Một sợi dây đang có sóng dừng ổn định. Sóng truyền trên dây có tần số \(10{\rm{ }}Hz\) và bước sóng \(6{\rm{ }}cm\) . Trên dây, hai phần tử \(M\) và \(N\) có vị trí cân bằng cách nhau \(8{\rm{ }}cm\), \(M\) thuộc một bụng sóng dao động điều hòa với biên độ \(6{\rm{ }}mm\). Lấy \({\pi ^2} = 10\). Tại thời điểm t, phần tử \(M\) đang chuyển động với tốc độ \(6\pi {\rm{ }}\left( {cm/s} \right)\) thì phần tử \(N\) chuyển động với gia tốc có độ lớn là:
Trả lời bởi giáo viên
Bước sóng 6 cm nên chiều dài 1 bó sóng là 3 cm. M thuộc bụng sóng và MN = 8 cm nên ta suy được vị trí của N như hình vẽ. Từ vị trí của N ta suy ra N dao động ngược pha với M.
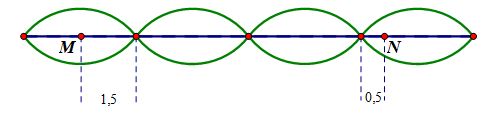
N cách điểm nút gần nhất 1 khoảng x = 0,5 cm nên biên độ của N: \({A_N} = {A_M}\left| {\cos \left( {\frac{{2\pi x}}{\lambda } - \frac{\pi }{2}} \right)} \right| = \frac{{{A_M}}}{2} = 3(mm)\).
Vận tốc cực đại của M: \({v_{\max }} = 2{A_M}\pi f = 12\pi (cm/s)\).
Thời điểm t, vM = vmax/2 suy ra \({x_M} = \pm \frac{{{A_M}\sqrt 3 }}{2}\). Vì N ngược pha M nên có \({x_N} = \mp \frac{{{A_N}\sqrt 3 }}{2}\).
Độ lớn gia tốc của N tại t: \(\left| {{a_N}} \right| = {\omega ^2}\left| {{x_N}} \right| = 4{\pi ^2}{f^2}.\frac{{\sqrt 3 }}{2}{A_N} = 6\sqrt 3 (m/{s^2})\).
Hướng dẫn giải:
+ Sử dụng phương trình sóng
+ Sử dụng biểu thức tính vận tốc cực đại: \({v_{{\rm{max}}}} = \omega A = 2\pi fA\)
+ Sử dụng biểu thức tính gia tốc: \(\left| a \right| = {\omega ^2}\left| x \right|\)

