Thực hiện giao thoa sóng cơ với hai nguồn hoàn toàn giống nhau. Hai nguồn đặt tại hai điểm $A$ và $B$, với $B$ cố định còn $A$ thay đổi được. Ban đầu khi thực hiện giao thoa thì thấy với $M$ cách $A$ một khoảng \({d_A} = {\rm{ }}28cm\), cách $B$ một khoảng \({d_B} = {\rm{ }}32cm\) là một điểm cực đại giao thoa. Sau đó người ta dịch chuyển điểm $A$ ra xa điểm $B$ dọc theo đường thẳng nối hai điểm $A$ và $B$ thì thấy có $2$ lần điểm $M$ là cực đại giao thoa, lần thứ $2$ thì đường cực đại qua $M$ là dạng đường thẳng và vị trí $A$ lúc này cách vị trí ban đầu một khoảng \(x{\rm{ }} = {\rm{ }}12cm\). Hãy xác định số điểm cực đại trong khoảng nối giữa $A$ và $B$ khi chưa dịch chuyển nguồn?
Trả lời bởi giáo viên
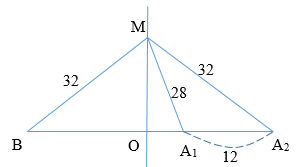
- Ban đầu: $\Delta {d_1} = k.\lambda \to 32 - 28 = 4 = k.\lambda $ (1)
- Sau khi dịch chuyển $A$: \(\Delta {d_2} = \left( {k - 2} \right).\lambda \) (2)
+ Đường cực đại qua $M$ là đường thẳng
\( \to k{\text{ }} - 2{\text{ }} = {\text{ }}0 \to k{\text{ }} = 2\)
Thay vào (1), ta suy ra: \(\lambda = 2cm\)
Từ hình ta có: ${\rm{cos}}\widehat {M{A_2}{A_1}} = \dfrac{{MA_1^2 - MA_2^2 - {A_1}A_2^2}}{{ - 2M{A_2}.{A_1}{A_2}}} = \dfrac{{{{28}^2} - {{32}^2} - {{12}^2}}}{{ - 2.32.12}} = \dfrac{1}{2} = \dfrac{{O{A_2}}}{{M{A_2}}}$
Ta suy ra: \(O{A_2} = \dfrac{{M{A_2}}}{2} = \dfrac{{32}}{2} = 16 = OB\)
\(\begin{array}{l} \to OM = \sqrt {M{B^2} - O{B^2}} = \sqrt {{{32}^2} - {{16}^2}} = 16\sqrt 3 cm\\ \to O{A_1} = \sqrt {MA_1^2 - O{M^2}} = \sqrt {{{28}^2} - {{\left( {16\sqrt 3 } \right)}^2}} = 4cm\\ \to B{A_1} = OB + O{A_1} = 16 + 4 = 20cm\end{array}\)
Số cực đại trên khoảng \(B{A_1}\):
\(\begin{array}{l} - \dfrac{{B{A_1}}}{\lambda } < k < \dfrac{{B{A_1}}}{\lambda } \leftrightarrow - \dfrac{{20}}{2} < k < \dfrac{{20}}{2} \leftrightarrow - 10 < k < 10\\ \to k = 0, \pm 1, \pm 2,..., \pm 9\end{array}\)
=> Số cực đại trên khoảng \(B{A_1}\) là $19$ điểm
Hướng dẫn giải:
+ Sử dụng điều kiện cực đại của hai nguồn cùng pha: \({d_2} - {d_1} = k\lambda \)
+ Sử dụng biểu thức tính số cực đại của hai nguồn cùng pha: $ - \dfrac{{AB}}{\lambda } < k < \dfrac{{AB}}{\lambda }$

