Một nguồn âm tại \(O\) xem như nguồn điểm cho mức cường độ âm tại \(A\) là \({L_A} = 30dB\), mức cường độ âm tại \(B\) là \({L_B} = 40dB\). Biết \(OA\) và \(OB\) vuông góc với nhau. Bỏ qua sự hấp thụ âm của môi trường. Nếu đặt tại \(O\) thêm \(9\) nguồn âm giống như nguồn âm trên thì mức cường độ âm tại trung điểm của đoạn AB gần nhất với giá trị nào sau đây?
Trả lời bởi giáo viên
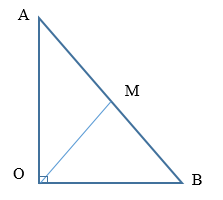
Ta có:
\(\begin{array}{l}{L_B} - {L_A} = 10\log \dfrac{{r_A^2}}{{r_B^2}}\\ \leftrightarrow 40 - 30 = 10\log \dfrac{{r_A^2}}{{r_B^2}}\\ \to \dfrac{{r_A^2}}{{r_B^2}} = {10^1} \to {r_A} = \sqrt {10} {r_B}\end{array}\)
Đặt ${r_B} = OB = a \to OA = {r_A} = \sqrt {10} a$
\( \to AB = \sqrt {O{B^2} + O{A^2}} = \sqrt {11} a\)
Vì \(\Delta ABO\) vuông tại $O$
Đường trung tuyến: \(OM = \dfrac{1}{2}AB = \dfrac{{\sqrt {11} a}}{2}\)
\({L_{{M_1}}}\) - mức cường độ âm khi tại $O$ có $1$ nguồn âm
\({L_{{M_2}}}\) - mức cường độ âm khi tại $O$ có $10$ nguồn âm
Ta có:
\(\begin{array}{l}{L_B} - {L_{{M_1}}} = 10\log \dfrac{{O{M^2}}}{{O{B^2}}} = 10\log \dfrac{{{{\left( {\dfrac{{\sqrt {11} a}}{2}} \right)}^2}}}{{{a^2}}} = 4,39dB\\ \to {L_{{M_1}}} = {L_B} - 4,39 = 40 - 4,39 = 35,6dB\end{array}\)
Mặt khác, ta có:
\(\begin{array}{l}{L_{{M_1}}} = 10\log \dfrac{{{I_{{M_1}}}}}{{{I_0}}} \leftrightarrow 35,6 = 10\log \dfrac{{{I_{{M_1}}}}}{{{I_0}}}\\ \to {I_{{M_1}}} = {10^{\dfrac{{35,6}}{{10}}}}{I_0} = 3630,8{I_0}\end{array}\)
Lại có: \(I = \dfrac{P}{{4\pi {r^2}}}\)
Ta suy ra: \(\dfrac{{{I_{{M_1}}}}}{{{I_{{M_2}}}}} = \dfrac{{{P_1}}}{{{P_2}}} = \dfrac{P}{{10P}} = \dfrac{1}{{10}} \to {I_{{M_2}}} = 10{I_{{M_1}}} = 36308{I_0}\)
\( \to {L_{{M_2}}} = 10\log \dfrac{{{I_{{M_2}}}}}{{{I_0}}} = 10\log \dfrac{{36308{I_0}}}{{{I_0}}} = 45,6dB\)
Hướng dẫn giải:
+ Sử dụng biểu thức hiệu mức cường độ âm: \({L_A} - {L_B} = 10\log \dfrac{{{I_A}}}{{{I_B}}} = 10\log \dfrac{{r_B^2}}{{r_A^2}} = 20\log \dfrac{{{r_B}}}{{{r_A}}}\)
+ Sử dụng biểu thức tính mức cường độ âm: \(L = 10\log \dfrac{I}{{{I_0}}}\)
+ Vận dụng biểu thức tính cường độ âm: \(I = \dfrac{P}{{4\pi {r^2}}}\)

