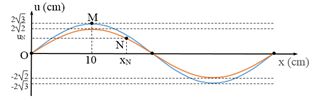
Sóng dừng trên một sợi dây với biên độ điểm bụng là \(4{\rm{ }}cm\). Hình bên biểu diễn hình dạng sợi dây tại hai thời điểm \({t_1}\) và \({t_2}\). Ở thời điểm \({t_1}\) điểm bụng M đang chuyển động với tốc độ bằng tốc độ chuyển động của điểm N ở thời điểm \({t_2}\) . Tọa độ của điểm N tại thời điểm \({t_2}\) là:

Trong đêm hoan ca văn nghệ kỉ niệm $45$ năm ngày thành lập trường THPT Thanh Oai B. Mở màn đêm diễn là lớp $12A2$, coi mọi học sinh đều hát với cùng cường độ âm và cùng tần số. Khi một học sinh hát thì mức cường độ âm là \(68{\rm{ }}dB\). Khi cả đội cùng hát thì đo được mức cường độ âm là \(80{\rm{ }}dB\). Số học sinh lớp $12A2$ có trong tốp ca này là:

Một sóng cơ học truyền trên sợi dây dài nằm ngang với bước sóng \(\lambda  = {\rm{ }}20{\rm{ }}cm\) và biên độ dao động \(A{\rm{ }} = {\rm{ }}4cm\) không đổi khi truyền đi. Gọi \(MN\) là hai điểm trên dây cách nhau một đoạn \(25cm\)  theo phương ngang. Tính khoảng cách lớn nhất và nhỏ nhất giữa hai điểm \(MN\) ?

Trên một sợi dây dài \(30{\rm{ }}cm\), hai đầu cố định đang có sóng dừng. Trên dây có tất cả \(2\) điểm \(M,{\rm{ }}N\) luôn dao động với biên độ cực đại là \(2{\rm{ }}cm\). Chọn phương án chính xác nhất.

Trên một sợi dây \(AB\) dài \(1,2{\rm{ }}m\) đang có sóng dừng với \(3\) bụng sóng, biên độ bụng sóng \(a = 4\sqrt 2 cm\) . Tốc độ truyền sóng trên dây \(v{\rm{ }} = {\rm{ }}80{\rm{ }}cm/s\). Biết hai đầu \(A,{\rm{ }}B\) là các nút sóng. Ở thời điểm phần tử tại điểm \(M\) trên dây cách \(A\) \(30{\rm{ }}cm\) có li độ \(2{\rm{ }}cm\) thì phần tử tại điểm \(N\) trên dây cách \(B\) \(50{\rm{ }}cm\) có tốc độ là:

Trong thí nghiệm giao thoa sóng nước, hai nguồn \({S_1}\) và \({S_2}\) cách nhau \(16cm\), dao động theo phương vuông góc với mặt nước, cùng biên độ, cùng pha, cùng tần số \(80Hz\). Tốc độ truyền sóng trên mặt nước là \(40cm/s\). Ở mặt nước, gọi \(\Delta \) là đường trung trực của đoạn \({S_1}{S_2}\) . Trên \(\Delta \)  điểm \(M\) cách \({S_1}\) \(10cm\), điểm \(N\) dao động cùng pha với \(M\) và gần \(M\) nhất sẽ cách \(M\) một đoạn:

Một sợi dây đang có sóng dừng ổn định. Sóng truyền trên dây có tần số \(10{\rm{ }}Hz\) và bước sóng \(6{\rm{ }}cm\) . Trên dây, hai phần tử \(M\) và \(N\) có vị trí cân bằng cách nhau \(8{\rm{ }}cm\), \(M\) thuộc một bụng sóng dao động điều hòa với biên độ \(6{\rm{ }}mm\). Lấy \({\pi ^2} = 10\). Tại thời điểm t, phần tử \(M\) đang chuyển động với tốc độ \(6\pi {\rm{ }}\left( {cm/s} \right)\) thì phần tử \(N\) chuyển động với gia tốc có độ lớn là:

Cho \(4\) điểm \(O,{\rm{ }}M,{\rm{ }}N\) và \(P\) nằm trong một môi trường truyền âm. Trong đó, \(M\) và \(N\) nằm trên nửa đường thẳng xuất phát từ \(O\), tam giác \(MNP\) là tam giác đều. Tại \(O\), đặt một nguồn âm điểm có công suất không đổi, phát âm đẳng hướng ra môi trường. Coi môi trường không hấp thụ âm. Biết mức cường độ âm tại \(M\) và \(N\) lần lượt là \(50{\rm{ }}dB\) và \(40{\rm{ }}dB\). Mức cường độ âm tại P là: