Tại mặt nước có hai nguồn sóng \(A,{\rm{ }}B\) giống hệt nhau cách nhau \(8cm\), gọi \(M,{\rm{ }}N\) là hai điểm trên mặt nước sao cho \(MN = 4cm\) và tạo với \(AB\)một hình thang cân \(\left( {MN//AB} \right)\), biết \(M,{\rm{ }}N\) dao động với biên độ cực đại. Bước sóng trên mặt nước là \(1cm\). Để trên đoạn \(MN\) có đúng \(5\) điểm dao động cực đại thì diện tích của hình thang phải là:
Trả lời bởi giáo viên
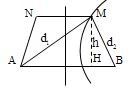
Để trên đoạn \(MN\) có \(5\) cực đại thì M phải thuộc cực đại bậc \(2\) nên \(k{\rm{ }} = {\rm{ }}2\)
M là cực đại thì \({{\rm{d}}_1} - {d_2} = k\lambda = 2.1 = 2cm(1)\)
Xét tam giác \(AHM\)có:
\(d_1^2 = A{M^2} = A{H^2} + H{M^2} = {(AO + OH)^2} + {h^2} = {\left( {\frac{{AB}}{2} + OH} \right)^2} + {h^2} = {6^2} + {h^2}\left( 2 \right)\)
Tương tự xét tam giác \(BMH\) có:
\(d_2^2 = B{M^2} = B{H^2} + H{M^2} = {\left( {OB - OH} \right)^2} + {h^2} = {\left( {\frac{{AB}}{2} - OH} \right)^2} + {h^2} = {2^2} + {h^2}\left( 3 \right)\)
Lấy (2) trừ (3) vế theo vế ta có: \({\rm{d}}_1^2 - d_2^2 = 32\left( 4 \right)\) từ (1) thay vào (4) suy ra:
\(\left( {{d_1} - {d_2}} \right)\left( {{d_1} + {d_2}} \right) = 32 \Rightarrow {d_1} + {d_2} = \frac{{32}}{{{d_1} - {d_2}}} = \frac{{32}}{2} = 16cm\)
Vậy ta có hệ: \(\left\{ \begin{array}{l}{d_1} - {d_2} = 2\\{d_1} + {d_2} = 16\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{d_1} = 9cm\\{d_2} = 7cm\end{array} \right.\) Thay vào (2) suy ra: \(h = 3\sqrt 5 cm\)
Vậy diện tích lớn nhất của hình thang: \(S = \frac{1}{2}.h\left( {AB + MN} \right) = 18\sqrt 5 c{m^2}\).
Hướng dẫn giải:
+ Sử dụng điều kiện cực đại của hai nguồn cùng pha: \({d_2} - {d_1} = k\lambda \)
+ Vận dụng các hệ thức trong tam giác
+ Sử dụng công thức tính diện tích hình thang: \(S = \frac{1}{2}\)(đáy lớn + đáy nhỏ).chiều cao

