Câu hỏi:
2 năm trước
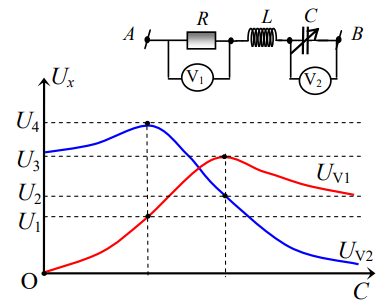
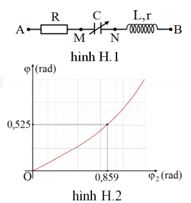
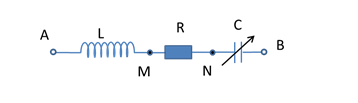
Đoạn mạch gồm một cuộn dây có điện trở \(R\) và độ tự cảm L nối tiếp với một tụ điện biến đổi có điện dung thay đổi được . Điện áp xoay chiều ở hai đầu đoạn mạch là \(u = U\sqrt 2 cos\left( {\omega t} \right)V\). Khi \(C{\rm{ }} = {\rm{ }}{C_1}\) thì công suất mạch là \(P{\rm{ }} = {\rm{ }}200W\) và cường độ dòng điện qua mạch là \(i = I\sqrt 2 cos\left( {\omega t + \dfrac{\pi }{3}} \right)A\). Khi \(C{\rm{ }} = {\rm{ }}{C_2}\) thì công suất cực đại. Công suất của mạch khi \(C{\rm{ }} = {\rm{ }}{C_2}\) là:
Trả lời bởi giáo viên
Đáp án đúng: c
- Khi \(C = {C_1}\) :
+ Khi \(C = {C_1}\) ta có độ lệch pha của \(u\) so với \(i\) là: \(\varphi = 0 - \dfrac{\pi }{3} = - \dfrac{\pi }{3}\)
Mặt khác, ta có:
\(\begin{array}{l}\tan \varphi = \dfrac{{{Z_L} - {Z_{{C_1}}}}}{R}\\ \leftrightarrow \tan \left( { - \dfrac{\pi }{3}} \right) = \dfrac{{{Z_L} - {Z_{{C_1}}}}}{R}\end{array}\)
\( \to {Z_{{C_1}}} - {Z_L} = \sqrt 3 R\) (1)
+ Công suất của mạch khi đó: \({P_1} = \dfrac{{{U^2}}}{{Z_1^2}}R = \dfrac{{{U^2}}}{{{R^2} + {{\left( {{Z_L} - {Z_{{C_1}}}} \right)}^2}}}R\) (2)
Thay (1) vào (2), ta được: \({P_1} = \dfrac{{{U^2}}}{{{R^2} + 3{R^2}}}R = \dfrac{{{U^2}}}{{4R}}\) (3)
- Khi\(C = {\rm{ }}{C_2}\):
+ Khi \(C = {C_2}\) thì công suất cực đại => Mạch xảy ra cộng hưởng \( \to {Z_L} = {Z_{{C_2}}}\)
+ Công suất khi đó: \({P_2} = \dfrac{{{U^2}}}{R}\) (4)
Lấy \(\dfrac{{\left( 3 \right)}}{{\left( 4 \right)}}\) ta được: \(\dfrac{{{P_1}}}{{{P_2}}} = \dfrac{1}{4} \to {P_2} = 4{P_1} = 4.200 = 800W\)
Hướng dẫn giải:
+ Sử dụng biểu thức tính độ lệch pha của u so với i: \(\tan \varphi = \dfrac{{{Z_L} - {Z_C}}}{R}\)
+ Sử dụng biểu thức tính công suất: \(P = UIcos\varphi = \dfrac{{{U^2}}}{{{Z^2}}}R\)
+ C biến thiên để \({P_{max}}\) => cộng hưởng điện
Câu hỏi khác
- Bài tập mạch RLC mắc nối tiếp có lời giải MÔN LÝ lớp 12
- Bài tập các mạch điện xoay chiều có lời giải MÔN LÝ lớp 12
- Bài tập pha u,i - viết phương trình u, i có lời giải MÔN LÝ lớp 12
- Bài tập lý thuyết đại cương về dòng điện xoay chiều có lời giải MÔN LÝ lớp 12
- Bài tập đại cương dòng điện xoay chiều có lời giải MÔN LÝ lớp 12
