Câu hỏi:
2 năm trước
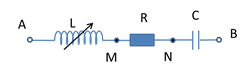
Cho mạch điện gồm R, L, C mắc nối tiếp. Cho \(R = 80\Omega ,{\rm{ }}C = \dfrac{{200}}{\pi }\mu F\), L thay đổi được. Đặt vào hai đầu mạch điện một điện áp xoay chiều \(u = 160cos(100\pi t + \dfrac{\pi }{3})V\). Khi \(L = {L_0}\) thì điện áp hiệu dụng giữa hai đầu điện trở đạt giá trị cực đại. Khi đó, biểu thức điện áp giữa hai đầu tụ điện là:
Trả lời bởi giáo viên
Đáp án đúng: b
- Ta có: L biến thiên để \({U_{Rmax}}\) khi mạch xảy ra hiện tượng cộng hưởng điện: \({Z_L} = {Z_C}\)
+ Cường độ dòng điện cực đại khi đó: \({I_0} = \dfrac{{{U_0}}}{R} = \dfrac{{160}}{{80}} = 2(A)\)
+ Mạch xảy cộng hưởng => u, i cùng pha \( \to {\varphi _i} = {\varphi _u} = \dfrac{\pi }{3}\left( {rad} \right)\)
- Dung kháng: \({Z_C} = \dfrac{1}{{\omega C}} = \dfrac{1}{{100\pi .\dfrac{{{{200.10}^{ - 6}}}}{\pi }}} = 50\Omega \)
- Hiệu điện thế cực đại giữa hai đầu tụ điện: \({U_{0C}} = {I_0}{Z_C} = 2.50 = 100(V)\)
- Mặt khác, ta có \({u_C}\) chậm pha hơn \(i\) một góc \(\dfrac{\pi }{2}(ra{\rm{d}})\)
\( \to {\varphi _{{u_C}}} = {\varphi _i} - \dfrac{\pi }{2} = \dfrac{\pi }{3} - \dfrac{\pi }{2} = - \dfrac{\pi }{6}\left( {rad} \right)\)
=> Biểu thức điện áp giữa hai đầu cuộn cảm: \({u_C} = 100c{\rm{os}}\left( {100\pi t - \dfrac{\pi }{6}} \right)V\)
Hướng dẫn giải:
- Bài toán L biến thiên để URmax (mạch cộng hưởng điện), khi đó:
+ Cường độ dòng điện cực đại trong mạch: \({I_0} = \dfrac{{{U_0}}}{R}\)
+ u, i cùng pha với nhau
- Sử dụng biểu thức tính dung kháng: \({Z_C} = \dfrac{1}{{\omega C}}\)
- Sử dụng biểu thức tính hiệu điện thế cực đại: \({U_0} = {I_0}Z\)
- \({u_C}\) chậm pha hơn \(i\) một góc \(\dfrac{\pi }{2}\)
- Viết biểu thức điện áp giữa hai đầu tụ điện: \({u_C} = {U_{0C}}cos\left( {\omega t + {\varphi _{uC}}} \right)\)
Câu hỏi khác
- Bài tập mạch RLC mắc nối tiếp có lời giải MÔN LÝ lớp 12
- Bài tập các mạch điện xoay chiều có lời giải MÔN LÝ lớp 12
- Bài tập pha u,i - viết phương trình u, i có lời giải MÔN LÝ lớp 12
- Bài tập lý thuyết đại cương về dòng điện xoay chiều có lời giải MÔN LÝ lớp 12
- Bài tập đại cương dòng điện xoay chiều có lời giải MÔN LÝ lớp 12
