Câu hỏi:
2 năm trước
Mạch dao động có tụ điện \(10nF\) và cuộn cảm \(4mH\). Tại thời điểm ban đầu dòng điện qua cuộn dây bằng dòng hiệu dụng và đang giảm. Ở thời điểm nào ngay sau đó, năng lượng điện bằng 3 lần năng lượng từ. Lấy \({\pi ^2} = 10\).
Trả lời bởi giáo viên
Đáp án đúng: b
+ Chu kì dao động của mạch: \(T = 2\pi \sqrt {LC} = {4.10^{ - 5}}s\)
+ Tại thời điểm ban đầu: \({i_1} = I = \dfrac{{{I_0}}}{{\sqrt 2 }}\)
Thời điểm năng lượng điện bằng 3 lần năng lượng từ: \({\rm{W}} = {{\rm{W}}_L} + {{\rm{W}}_C} = 4{W_L} \Leftrightarrow 4\dfrac{{Li_2^2}}{2} = \dfrac{{LI_0^2}}{2} \Rightarrow {i_2} = \pm \dfrac{{{I_0}}}{2}\)
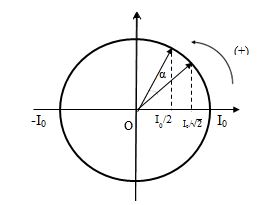
Dựa vào hình vẽ ta tính được góc quét \(\alpha = \dfrac{\pi }{3} - \dfrac{\pi }{4} = \dfrac{\pi }{{12}}rad\)
Thời điểm ngay sau đó năng lượng điện bằng 3 lần năng lượng từ là:
\(\Delta t = \dfrac{\alpha }{\omega } = \dfrac{\pi }{{12}}.\dfrac{T}{{2\pi }} = \dfrac{T}{{24}} = \dfrac{5}{3}\mu s\)
Hướng dẫn giải:
+ Sử dụng biểu thức tính chu kì dao động của mạch LC: \(T = 2\pi \sqrt {LC} \)
+ Sử dụng lí thuyết về năng lượng điện từ trong mạch LC và áp dụng vòng tròn lượng giác để tính thời gian
Câu hỏi khác
- Bài tập mạch dao động LC các đại lượng đặc trưng có lời giải MÔN LÝ lớp 12
- Bài tập năng lượng của mạch dao động LC có lời giải MÔN LÝ lớp 12
- Bài tập phương trình dao động mạch LC q,u,i có lời giải MÔN LÝ lớp 12
- Bài tập điện từ trường - sóng điện từ lý 12 có lời giải
- Bài tập các loại dao động lý 12 có lời giải
