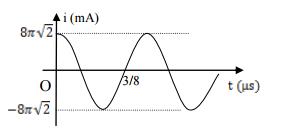
Một tụ điện có điện dung \(C = 5nF\) gồm hai bản A và B được nối với nguồn điện không đổi có suất điện động \(E{\rm{ }} = {\rm{ }}8{\rm{ }}V\), bản A nối với cực dương, còn bản B nối với cực âm. Sau đó, ngắt tụ ra khỏi nguồn và nối tức thời hai bản tụ với cuộn cảm thuần có độ tự cảm \(L = 50\mu H\). Tính từ lúc nối điện khi điện tích của bản B bằng \(20{\rm{ }}nC\) và bản tụ này đang ở trạng thái phóng điện thì mất thời gian ngắn nhất là:
Trả lời bởi giáo viên
+ Chu kì của mạch dao động: \(T = 2\pi \sqrt {LC} = 2\pi \sqrt {{{50.10}^{ - 6}}{{.5.10}^{ - 9}}} = \pi {10^{ - 6}}\left( s \right) = \pi \left( {\mu s} \right)\)
+ Điện tích cực đại trên mỗi bản tụ: \({Q_0} = C{U_0} = C.E = 5.8 = 40{\rm{ }}nC\)
+ Ban đầu: Bản B nối với cực âm ta suy ra: \({q_B} = - {Q_0} = - 40nC\)
Biểu diễn trên đường tròn lượng giác ta có:
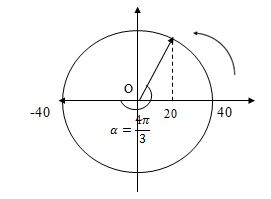
Thời gian ngắn nhất để \({q_B} = - {Q_0}\) đến \({q_B} = 20nC = \dfrac{{{Q_0}}}{2}\) (phóng điện) là: \(\Delta t = \dfrac{\alpha }{\omega } = \dfrac{{4\pi }}{3}.\dfrac{T}{{2\pi }} = \dfrac{{2T}}{3} = 2,1\mu s\)
Hướng dẫn giải:
+ Sử dụng biểu thức tính chu kì dao động của mạch: \(T = 2\pi \sqrt {LC} \)
+ Vận dụng biểu thức tính điện tích cực đại: \({Q_0} = C{U_0} = CE\)
+ Sử dụng đường tròn lượng giác và công thức tính thời gian: \(\Delta t = \dfrac{{\Delta \varphi }}{\omega }\) (\(\Delta \varphi \) là góc quét được trong thời gian \(\Delta t\))