Câu hỏi:
2 năm trước
Trong một mạch dao động LC lí tưởng đang có dao động điện từ tự do. Khoảng thời gian ngắn nhất để cường độ dòng điện qua cuộn cảm giảm từ độ lớn cực đại xuống còn một nửa độ lớn cực đại là \(800\mu s\). Khoảng thời gian ngắn nhất để năng lượng từ trường trong mạch giảm từ độ lớn cực đại xuống còn một nửa giá trị đó là :
Trả lời bởi giáo viên
Đáp án đúng: c
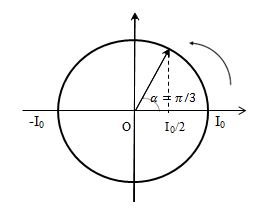
- Khoảng thời gian để cường độ dòng điện qua cuộn cảm giảm từ độ lớn cực đại xuống còn một nửa độ lớn cực đại là: \(\Delta t = \dfrac{\alpha }{\omega } = \dfrac{\pi }{3}.\dfrac{T}{{2\pi }} = \dfrac{T}{6} = 800\mu s \Rightarrow T = 4800\mu s\)
- Năng lượng từ trường trong mạch cực đại: \(i = \pm {I_0}\)
- Năng lượng từ trường bằng nửa giá trị cực đại: \(\dfrac{{L{i^2}}}{2} = \dfrac{1}{2}.\dfrac{{LI_0^2}}{2} \Rightarrow i = \pm \dfrac{{{I_0}}}{{\sqrt 2 }}\)
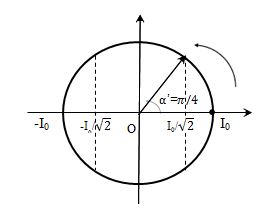
=> Khoảng thời gian ngắn nhất để năng lượng từ trường trong mạch giảm từ độ lớn cực đại xuống còn một nửa giá trị đó là: \(\Delta t' = \dfrac{{\alpha '}}{\omega } = \dfrac{\pi }{4}.\dfrac{T}{{2\pi }} = \dfrac{T}{8} = \dfrac{{4800}}{8} = 600\mu s\)
Hướng dẫn giải:
Sử dụng lí thuyết về dao động điện từ; vòng tròn lượng giác và công thức tính thời gian: \(\Delta t = \dfrac{\alpha }{\omega }\) (\(\alpha \) là góc quét được trong thời gian \(\Delta t\))
Câu hỏi khác
- Bài tập mạch dao động LC các đại lượng đặc trưng có lời giải MÔN LÝ lớp 12
- Bài tập năng lượng của mạch dao động LC có lời giải MÔN LÝ lớp 12
- Bài tập phương trình dao động mạch LC q,u,i có lời giải MÔN LÝ lớp 12
- Bài tập điện từ trường - sóng điện từ lý 12 có lời giải
- Bài tập các loại dao động lý 12 có lời giải
