Câu hỏi:
2 năm trước
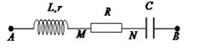
Trên đoạn mạch xoay chiều không phân nhánh có bốn điểm theo đúng thứ tự A, M, N và B. Giữa 2 điểm A và M chỉ có cuộn dây, giữa 2 điểm M và N chỉ có điện trở thuần R, giữa 2 điểm N và B chỉ có tụ điện. Điện áp hiệu dụng trên AB, AN và MN thỏa mãn hệ thức \({U_{AB}} = {U_{AN}} = {U_{MN}}\sqrt 3 = 120\sqrt 3 V\). Dòng điện hiệu dụng dụng trong mạch có giá trị là \(2\sqrt 2 A\). Điện áp tức thời trên đoạn AN và trên đoạn AB lệch pha nhau một góc đúng bằng góc lệch pha giữa điện áp tức thời trên AM và dòng điện. Cảm kháng của cuộn dây có giá trị là:
Trả lời bởi giáo viên
Đáp án đúng: b
Ta có:
Gọi độ lệch pha giữa điện áp tức thời trên đoạn AN và trên đoạn AB là \(2\alpha \)
=> góc lệch pha giữa điện áp tức thời trên AM và dòng điện cũng là \(2\alpha \)
Vẽ trên giản đồ véc-tơ ta được:
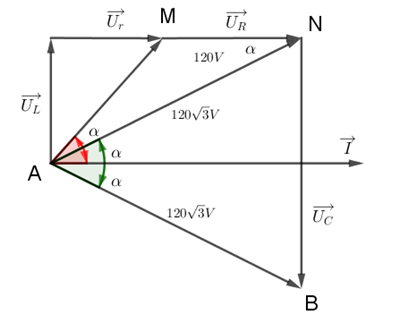
Ta có:
Tam giác AMN cân tại M (do \(\widehat {MAN} = \widehat {MNA}\) )
\( \Rightarrow AM = MN = 120\)
Xét \(\Delta AMN\), có:
\(\begin{array}{l}A{M^2} = M{N^2} + A{N^2} - 2MN.AN.cos\alpha \\ \Leftrightarrow {120^2} = {120^2} + {\left( {120\sqrt 3 } \right)^2} - 2.120.120\sqrt 3 .cos\alpha \\ \Rightarrow cos\alpha = \dfrac{{\sqrt 3 }}{2}\\ \Rightarrow \alpha = {30^0}\end{array}\)
+ Xét \(\Delta ANI\), có:
\(\begin{array}{l}\sin \alpha = \dfrac{{NI}}{{AN}} = \dfrac{{{U_L}}}{{AN}}\\ \Rightarrow {U_L} = AN.\sin \alpha = 120\sqrt 3 .\sin 30 = 60\sqrt 3 V\end{array}\)
+ Cảm kháng: \({Z_L} = \dfrac{{{U_L}}}{I} = \dfrac{{60\sqrt 3 }}{{2\sqrt 2 }} = 15\sqrt 6 \Omega \)
Hướng dẫn giải:
Sử dụng phương pháp giản đồ véctơ
Câu hỏi khác
- Bài tập mạch RLC mắc nối tiếp có lời giải MÔN LÝ lớp 12
- Bài tập các mạch điện xoay chiều có lời giải MÔN LÝ lớp 12
- Bài tập pha u,i - viết phương trình u, i có lời giải MÔN LÝ lớp 12
- Bài tập lý thuyết đại cương về dòng điện xoay chiều có lời giải MÔN LÝ lớp 12
- Bài tập đại cương dòng điện xoay chiều có lời giải MÔN LÝ lớp 12
