Câu hỏi:
2 năm trước
Một đoạn mạch xoay chiều gồm cuộn dây mắc nối tiếp với tụ điện. Độ lệch pha giữa cường độ dòng điện trong mạch và điện áp hai đầu mạch là \(\dfrac{\pi }{3}\). Điện áp hiệu dụng giữa hai đầu tụ điện bằng \(\sqrt 3 \) lần điện áp hai đầu cuộn dây. Độ lệch pha của điện áp giữa hai đầu cuộn dây so với cường độ dòng điện trong mạch là:
Trả lời bởi giáo viên
Đáp án đúng: a
Ta có:
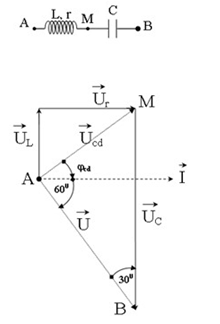
Xét \(\Delta AMB\) , có:
\(\begin{array}{l}\dfrac{{MB}}{{\sin \left( {{\varphi _{cd}} + {{60}^0}} \right)}} = \dfrac{{AM}}{{\sin {{30}^0}}}\\ \Leftrightarrow \dfrac{{{U_C}}}{{\sin \left( {{\varphi _{cd}} + {{60}^0}} \right)}} = \dfrac{{{U_{cd}}}}{{\sin {{30}^0}}}\\ \Leftrightarrow \dfrac{{\sqrt 3 {U_{cd}}}}{{\sin \left( {{\varphi _{cd}} + {{60}^0}} \right)}} = \dfrac{{{U_{cd}}}}{{\dfrac{1}{2}}}\\ \Rightarrow \sin \left( {{\varphi _{cd}} + {{60}^0}} \right) = \dfrac{{\sqrt 3 }}{2}\\ \Rightarrow \left[\begin{array}{l}{\varphi _{cd}} + {60^0} = {60^0} + k2\pi \\{\varphi _{cd}} + {60^0} = \left( {{{180}^0} - {{60}^0}} \right) + k2\pi \end{array} \right.\\ \Rightarrow \left[ \begin{array}{l}{\varphi _{cd}} = 0 + k2\pi \left( {loai} \right)\\{\varphi _{cd}} = {60^0} + k2\pi \end{array} \right.\end{array}\)
\( \Rightarrow {\varphi _{cd}} = {60^0} = \dfrac{\pi }{3}\)
Hướng dẫn giải:
Sử dụng giản đồ véctơ
Sử dụng định lí hàm số sin: \(\dfrac{a}{{{\mathop{\rm sinA}\nolimits} }} = \dfrac{b}{{{\mathop{\rm sinB}\nolimits} }} = \dfrac{c}{{{\mathop{\rm sinC}\nolimits} }}\)
Câu hỏi khác
- Bài tập các mạch điện xoay chiều có lời giải MÔN LÝ lớp 12
- Bài tập mạch RLC mắc nối tiếp có lời giải MÔN LÝ lớp 12
- Bài tập pha u,i - viết phương trình u, i có lời giải MÔN LÝ lớp 12
- Bài tập lý thuyết đại cương về dòng điện xoay chiều có lời giải MÔN LÝ lớp 12
- Bài tập đại cương dòng điện xoay chiều có lời giải MÔN LÝ lớp 12
