Câu hỏi:
2 năm trước
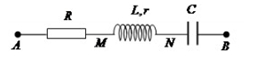
Trên đoạn mạch xoay chiều không phân nhánh có bốn điểm theo đúng thứ tự A, M, N và B. Giữa hai điểm A và M chỉ có điện trở \(R\), giữa hai điểm M và N có cuộn cảm có điện trở thuần \(r = 0,5R\)và độ tự cảm \(L = \dfrac{1}{\pi }H\), giữa hai điểm N và B chỉ có tụ điện có điện dung \(C = \dfrac{{50}}{\pi }\mu F\). Điện áp hiệu dụng trên đoạn AN là \(200V\). Điện áp trên đoạn MN lệch pha với điện áp trên AB là \(\dfrac{\pi }{2}\). Biểu thức điện áp trên \(AB\) là \({u_{AB}} = {U_0}cos\left( {100\pi t + \dfrac{\pi }{{12}}} \right)V\). Biểu thức điện áp trên NB là:
Trả lời bởi giáo viên
Đáp án đúng: b
Ta có:
+ Cảm kháng: \({Z_L} = \omega L = 100\pi .\dfrac{1}{\pi } = 100\Omega \)
Dung kháng: \({Z_C} = \dfrac{1}{{\omega C}} = \dfrac{1}{{100\pi .\dfrac{{50}}{\pi }{{.10}^{ - 6}}}} = 200\Omega = 2{Z_L}\)
Vẽ trên giản đồ, ta được:
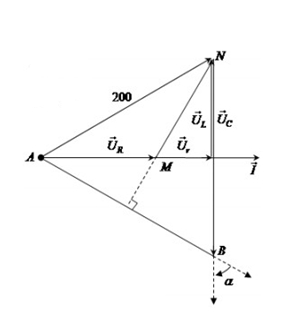
Ta có:
\(r = 0,5R \Rightarrow {U_r} = 0,5{U_R}\)
Lại có \({Z_C} = 2{Z_L} \Rightarrow {U_C} = 2{U_L}\)
Ta suy ra: \(\Delta ANB\) là \(\Delta \) đều
\(\begin{array}{l} \Rightarrow NB = AN \Leftrightarrow {U_C} = {U_{AN}} = 200V\\ \Rightarrow {U_{0C}} = 200\sqrt 2 V\end{array}\)
\(\alpha = \widehat {ABN} = {60^0}\) (2 góc đối đỉnh)
Từ giản đồ, ta có điện áp trên đoạn NB trễ pha so với điện áp trên AB một góc \(\alpha = {60^0} = \dfrac{\pi }{3}\)
\(\begin{array}{l} \Rightarrow {\varphi _{AB}} - {\varphi _{NB}} = \dfrac{\pi }{3}\\ \Rightarrow {\varphi _{NB}} = {\varphi _{AB}} - \dfrac{\pi }{3} = \dfrac{\pi }{{12}} - \dfrac{\pi }{3} = - \dfrac{\pi }{4}\left( {rad} \right)\end{array}\)
=> Phương trình điện áp trên đoạn NB: \({u_{NB}} = 200\sqrt 2 cos\left( {100\pi t - \dfrac{\pi }{4}} \right)V\)
Hướng dẫn giải:
+ Sử dụng biểu thức tính cảm kháng \({Z_L} = \omega L\) , dung kháng \({Z_C} = \dfrac{1}{{\omega C}}\)
+ Sử dụng giản đồ véc-tơ và các hệ thức trong tam giác
+ Viết phương trình điện áp: \(u = {U_0}cos\left( {\omega t + \varphi } \right)V\)
Câu hỏi khác
- Bài tập các mạch điện xoay chiều có lời giải MÔN LÝ lớp 12
- Bài tập mạch RLC mắc nối tiếp có lời giải MÔN LÝ lớp 12
- Bài tập pha u,i - viết phương trình u, i có lời giải MÔN LÝ lớp 12
- Bài tập lý thuyết đại cương về dòng điện xoay chiều có lời giải MÔN LÝ lớp 12
- Bài tập đại cương dòng điện xoay chiều có lời giải MÔN LÝ lớp 12
