Câu hỏi:
2 năm trước
Đặt điện áp xoay chiều \(u = 80c{\rm{os}}\omega {\rm{t}}\left( V \right)\)vào hai đầu đoạn mạch nối tiếp gồm điện trở R, cuộn cảm có độ tự cảm L, có điện trở thuần r và tụ điện C thì công suất tiêu thụ của mạch là \(40W\). Biết điện áp hiệu dụng trên điện trở, trên cuộn cảm và trên tụ điện lần lượt là 25V, 25V và 60V. Tổng giá trị điện trở trong mạch \(\left( {R + r} \right)\) là:
Trả lời bởi giáo viên
Đáp án đúng: a
Vẽ lại mạch điện và vẽ giản đồ véctơ, ta được:
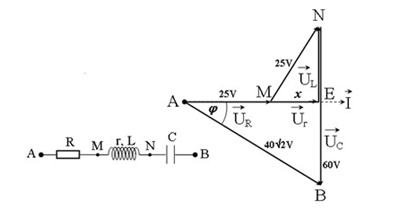
Từ giản đồ véctơ, ta có:
\(\begin{array}{l}N{E^2} = M{N^2} - M{E^2} = 625 - {x^2}\\ \to EB = 60 - \sqrt {625 - {x^2}} \\A{B^2} = A{E^2} + E{B^2} \leftrightarrow {\left( {40\sqrt 2 } \right)^2} = {\left( {25 + x} \right)^2} + {\left( {60 - \sqrt {625 - {x^2}} } \right)^2}\\ \to ... \to 120\sqrt {625 - {x^2}} = 1650 + 50{\rm{x}}\\ \to {\rm{12}}\sqrt {625 - {x^2}} = 165 + 5{\rm{x}}\\ \to {\rm{144}}\left( {625 - {x^2}} \right) = {\left( {165 + 5{\rm{x}}} \right)^2}\\ \to \left[ \begin{array}{l}x = 15\\x = - 24,76\end{array} \right.\\ \to x = 15 \Rightarrow AE = 40{\rm{V}}\\P = UIc{\rm{os}}\varphi {\rm{ = I}}{\rm{.AE}} \to I = \dfrac{P}{{AE}} = 1A\\ \to \left\{ \begin{array}{l}r = \dfrac{{{U_r}}}{I} = \dfrac{{15}}{1} = 15\Omega \\R = \dfrac{{{U_R}}}{I} = \dfrac{{25}}{1} = 25\Omega \end{array} \right.\\ \Rightarrow R + r = 25 + 15 = 40\Omega \end{array}\)
Hướng dẫn giải:
Sử dụng giản đồ véctơ
Câu hỏi khác
- Bài tập các mạch điện xoay chiều có lời giải MÔN LÝ lớp 12
- Bài tập mạch RLC mắc nối tiếp có lời giải MÔN LÝ lớp 12
- Bài tập pha u,i - viết phương trình u, i có lời giải MÔN LÝ lớp 12
- Bài tập lý thuyết đại cương về dòng điện xoay chiều có lời giải MÔN LÝ lớp 12
- Bài tập đại cương dòng điện xoay chiều có lời giải MÔN LÝ lớp 12
