Đối với dao động tuần hoàn, khoảng thời gian ngắn nhất mà sau đó trạng thái dao động của vật được lặp lại như cũ được gọi là:
Khoảng thời gian ngắn nhất mà sau đó trạng thái dao động của vật được lặp lại như cũ gọi là chu kì dao động của vật.
Chọn kết luận đúng khi nói về dao động điều hoà cuả con lắc lò xo:
A – sai vì: Vận tốc biến thiên điều hòa theo thời gian: \(v = \omega A\cos \left( {\omega t + \frac{\pi }{2}} \right)\)
B – sai vì: Gia tốc biến thiên điều hòa theo thời gian: \(a = {\omega ^2}Acos\left( {\omega t + \pi } \right)\)
C – đúng
D – sai vì: Quỹ đạo của vật dao động điều hòa là một đoạn thẳng
Một vật dao động được kích thích để dao động điều hòa với vận tốc cực đại bằng \(3{\rm{ }}m/s\) và gia tốc cực đại bằng \(30\pi \left( {m/{s^2}} \right)\). Thời điểm ban đầu \(t{\rm{ }} = {\rm{ }}0\) vật có vận tốc \(v{\rm{ }} = {\rm{ }} + {\rm{ }}1,5{\rm{ }}m/s\) và thế năng đang tăng. Hỏi sau đó bao lâu vật có gia tốc bằng \( - 15\pi \left( {m/{s^2}} \right)\)?
Ta có: \(\left\{ \begin{array}{l}{v_{{\rm{max}}}} = \omega A\\{a_{{\rm{max}}}} = {\omega ^2}A\end{array} \right. \to \left\{ \begin{array}{l}\dfrac{{{a_{{\rm{max}}}}}}{{{v_{{\rm{max}}}}}} = \omega = \dfrac{{30\pi }}{3} = 10\pi \\A = \dfrac{{{v_{{\rm{max}}}}}}{\omega } = \dfrac{3}{{10\pi }}m\end{array} \right.\)
Tại \(t{\rm{ }} = {\rm{ }}0:{\rm{ }}v{\rm{ }} = {\rm{ }} + 1,5m/s\) và thế năng đang tăng
Sử dụng hệ thức độc lập, ta có: \({A^2} = {x^2} + \dfrac{{{v^2}}}{{{\omega ^2}}} \to {x^2} = {A^2} - \dfrac{{{v^2}}}{{{\omega ^2}}} = {\left( {\dfrac{3}{{10\pi }}} \right)^2} - \dfrac{{{{1,5}^2}}}{{{{\left( {10\pi } \right)}^2}}} \to x = \dfrac{{1,5\sqrt 3 }}{{10\pi }} = \dfrac{{A\sqrt 3 }}{2}\)
Khi vật có gia tốc \(a = - 15\pi \left( {m/{s^2}} \right) = - {\omega ^2}{x_2} \to {x_2} = - \dfrac{{ - 15\pi }}{{{{\left( {10\pi } \right)}^2}}} = \dfrac{{1,5}}{{10\pi }} = \dfrac{A}{2}\)

=> Thời gian để vật đi từ \(t{\rm{ }} = 0\) đến vị trí có \(a{\rm{ }} = - 15\pi \left( {m/{s^2}} \right)\) là: \(t = \dfrac{T}{{12}} + \dfrac{T}{6} = \dfrac{T}{4} = \dfrac{1}{4}\dfrac{{2\pi }}{\omega } = 0,05s\)
Một con lắc đơn dao động điều hòa với biên độ góc \({\alpha _0}\) có \(cos{\alpha _0} = {\rm{ }}0,986\) . Khi vật đi qua vị trí có li độ góc α thì lực căng dây bằng trọng lực của vật. Giá trị \(cos\alpha \) bằng:
Ta có: lực căng dây được xác định bằng biểu thức:
\(\begin{array}{l}T = mg(3c{\rm{os}}\alpha {\rm{ - 2cos}}{\alpha _0}) = P = mg\\ \to 3c{\rm{os}}\alpha - {\rm{2cos}}{\alpha _0} = 1\\ \to c{\rm{os}}\alpha = \dfrac{{1 + 2c{\rm{os}}{\alpha _0}}}{3} = \dfrac{{1 + 2.0,986}}{3} = 0,99\end{array}\)
Chọn phát biểu sai khi nói về dao động điều hoà:
Ta có phương trình li độ, vận tốc, gia tốc của vật dao động điều hòa:
+ Li độ: \(x = Acos\left( {\omega t + \varphi } \right)\)
+ Vận tốc: \(v = \omega Ac{\rm{os}}\left( {\omega t + \varphi + \frac{\pi }{2}} \right)\)
+ Gia tốc: \(a = {\omega ^2}A\cos \left( {\omega t + \varphi + \pi } \right)\)
A, B, D – đúng
C – sai vì: Gia tốc sớm pha hơn vận tốc góc \(\frac{\pi }{2}\)
Trong dao động điều hoà, gia tốc biến đổi
Ta có phương trình vận tốc và gia tốc của vật dao động điều hòa:
+ Vận tốc: \(v = \omega Ac{\rm{os}}\left( {\omega t + \varphi + \dfrac{\pi }{2}} \right)\)
+ Gia tốc: \(a = {\omega ^2}A\cos \left( {\omega t + \varphi + \pi } \right)\)
=> Gia tốc biến đổi sớm pha \(\dfrac{\pi }{2}\) so với vận tốc
Đồ thị biểu diễn sự biến thiên của vận tốc theo li độ trong dao động điều hoà có dạng là:
Ta có: \({A^2} = {x^2} + \dfrac{{{v^2}}}{{{\omega ^2}}} \to \dfrac{{{x^2}}}{{{A^2}}} + \dfrac{{{v^2}}}{{{\omega ^2}{A^2}}} = 1\)
(Có dạng của phương trình elip \(\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1\) )
=> Đồ thị biểu diễn sự biến thiên của vận tốc theo li độ trong dao động điều hòa có dạng là đường elip
Sợi dây chiều dài \(l\), được cắt ra làm hai đoạn \({l_1}\) và \({l_2}\) dùng làm con lắc đơn. Biết li độ góc của con lắc đơn có chiều dài \({l_1}\) khi nó có động năng bằng thế năng, bằng li độ góc của con lắc đơn có chiều dài \({l_2}\) khi nó có động năng bằng hai lần thế năng. Vận tốc cực đại của con lắc đơn \({l_1}\) bằng hai lần vận tốc cực đại của con lắc \({l_2}\) . Tìm chiều dài \(l\) ban đầu:
Ta có:
Thế năng và cơ năng của con lắc: \({{\rm{W}}_t} = \dfrac{1}{2}mgl{\alpha ^2};{{\rm{W}}} = \dfrac{1}{2}mgl{\alpha _0}^2\)
+ Con lắc đơn có chiều dài \({l_1}\):
Khi \({{\rm{W}}_{\rm{d}}} = {{\rm{W}}_t} \to {\alpha _1} = \pm \dfrac{{{\alpha _{01}}}}{{\sqrt 2 }}\)
+ Con lắc đơn có chiều dài \({l_2}\):
Khi \({{\rm{W}}_{\rm{d}}} = 2{{\rm{W}}_t} \to {\alpha _2} = \pm \dfrac{{{\alpha _{02}}}}{{\sqrt 3 }}\)
Theo đầu bài, ta có: \({\alpha _1} = {\alpha _2} \to \dfrac{{{\alpha _{01}}}}{{\sqrt 2 }} = \dfrac{{{\alpha _{02}}}}{{\sqrt 3 }}\) (1)
Vận tốc cực đại của con lắc đơn: \({v_{{\rm{max}}}} = \omega {s_0} = \omega l{\alpha _0} = \sqrt {gl} {\alpha _0}\)
\({v_{{{\rm{1}}_{{\rm{max}}}}}} = 2{v_{{2_{{\rm{max}}}}}} \leftrightarrow \sqrt {g{l_1}} {\alpha _{01}} = 2\sqrt {g{l_2}} {\alpha _{02}}\) (2)
Từ (1) và (2), ta có: \({l_1}\dfrac{2}{3}\alpha _{02}^2 = 4{l_2}\alpha _{02}^2 \to {l_1} = 6{l_2}\)
=> Chiều dài \(l\) ban đầu: \(l{\rm{ }} = {\rm{ }}{l_1} + {\rm{ }}{l_2} = {\rm{ }}7{l_2}\)
Cho ba con lắc lò xo dao động điều hòa theo phương nằm ngang. Biết ba lò xo giống hệt nhau và vật nặng có khối lượng tương ứng \({m_1},{\rm{ }}{m_2},{\rm{ }}{m_3}\). Lần lượt kéo ba vật sao cho ba lò xo giãn cùng một đoạn A như nhau rồi thả nhẹ cho ba vật dao động điều hòa. Khi đi qua vị trí cân bằng vận tốc của hai vật \({m_1},{\rm{ }}{m_2}\) có độ lớn lần lượt là \({v_1} = {\rm{ }}20{\rm{ }}cm/s\), \({v_2} = {\rm{ }}10{\rm{ }}cm/s\). Biết \({m_3} = {\rm{ }}9{m_1} + {\rm{ }}4{m_2}\), độ lớn vận tốc cực đại của vật \({m_3}\) bằng :
+ Ba lò xo giống hệt nhau, đều có độ cứng là $k$, khối lượng của các vật nhỏ tương ứng là \({m_1},{\rm{ }}{m_2}\) và \({m_3}\)
+ Kéo $3$ lò xo ra khỏi VTCB một đoạn $A$ rồi thả nhẹ => Biên độ dao động của chúng giống nhau và bằng $A$
+ Ta có: \(\left\{ \begin{array}{l}{v_1} = {\omega _1}A = \sqrt {\dfrac{k}{{{m_1}}}} .A\\{v_2} = {\omega _2}A = \sqrt {\dfrac{k}{{{m_2}}}} .A\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{m_1} = \dfrac{{k{A^2}}}{{v_1^2}}\\{m_2} = \dfrac{{k{A^2}}}{{v_2^2}}\end{array} \right.\) ;
+ Theo đề bài ta có: \({m_3} = 9{m_1} + 4{m_2} = k{A^2}(\dfrac{9}{{v_1^2}} + \dfrac{4}{{v_2^2}})\)
=> Vận tốc của con lắc $3$ khi đi qua vị trí cân bằng :
\(\begin{array}{l}{v_1} = {\omega _1}A = \sqrt {\dfrac{k}{{{m_3}}}} .A = \sqrt {\dfrac{k}{{9{m_1} + 4{m_2}}}} A\\ = \sqrt {\dfrac{k}{{k{A^2}(\dfrac{9}{{v_1^2}} + \dfrac{4}{{v_2^2}})}}} .A = \sqrt {\dfrac{1}{{(\dfrac{9}{{v_1^2}} + \dfrac{4}{{v_2^2}})}}} = \sqrt {\dfrac{1}{{(\dfrac{9}{{{{20}^2}}} + \dfrac{4}{{{{10}^2}}})}}} = 4(cm/s)\end{array}\)
Một con lắc đơn dao động điều hòa, mốc thế năng tại vị trí cân bằng. Khi lực căng dây treo có độ lớn bằng trọng lực tác dụng lên vật nhỏ thì:
Trong dao động điều hòa của con lắc đơn thì
\(\begin{array}{l}1 - \cos \alpha = 2{\sin ^2}\dfrac{\alpha }{2} \approx {\dfrac{\alpha }{2}^2} \Rightarrow 1 - \cos \alpha \approx {\dfrac{\alpha }{2}^2}\\ \Rightarrow \left\{ \begin{array}{l}T = mg(3\cos \alpha - 2\cos {\alpha _0})\\P = mg\end{array} \right.\\ \Rightarrow (3\cos \alpha - 2\cos {\alpha _0}) = 1\\ \Rightarrow (3\cos \alpha - 2\cos {\alpha _0}) = 1\\ \Leftrightarrow 3\left( {1 - {{\dfrac{\alpha }{2}}^2}} \right) - 2\left( {1 - \dfrac{{\alpha _0^2}}{2}} \right) = 1\\ \Rightarrow \dfrac{{\alpha _0^2}}{{{\alpha ^2}}} = \dfrac{3}{2}(1)\\ \Rightarrow \left\{ \begin{array}{l}{\rm{W}} = \dfrac{1}{2}mgl\alpha _0^2\\{{\rm{W}}_t} = \dfrac{1}{2}mgl{\alpha ^2}\end{array} \right.\\ \Rightarrow \dfrac{{\rm{W}}}{{{{\rm{W}}_t}}} = \dfrac{{\alpha _0^2}}{{{\alpha ^2}}} = \dfrac{3}{2} \Leftrightarrow \dfrac{{{{\rm{W}}_d} + {{\rm{W}}_t}}}{{{{\rm{W}}_t}}} = \dfrac{3}{2}\\ \Rightarrow {{\rm{W}}_t} = 2{W_d}\end{array}\)
Một chất điểm có khối lượng \(m = 300g\) đồng thời thực hiện hai dao động điều hòa cùng phương, cùng tần số. Ở thời điểm $t$ bất kì li độ của hai dao động thành phần luôn thõa mãn \(16{\rm{x}}_1^2 + 9{\rm{x}}_2^2 = 25\) (\({x_1},{\rm{ }}{x_2}\) tính bằng cm). Biết lực phục hồi cực đại tác dụng lên chất điểm trong quá trình dao động là \({F_{ma{\rm{x}}}} = 0,4N\). Tần số góc của đao động có giá trị:
Từ giả thuyết :\(16{\rm{x}}_1^2 + 9{\rm{x}}_2^2 = 25 \Leftrightarrow {\left( {\dfrac{{{x_1}}}{{1,25}}} \right)^2} + {\left( {\dfrac{{{x_2}}}{{\dfrac{5}{3}}}} \right)^2} = 1\)
Hai dao động này vuông pha với các biên độ thành phần \({A_1} = 1,25cm\), \({A_2} = \dfrac{5}{3}cm\)
Biên độ dao động tổng hợp: \(A = \sqrt {A_1^2 + A_2^2} = \sqrt {{{1,25}^2} + {{\left( {\dfrac{5}{3}} \right)}^2}} = \dfrac{{25}}{{12}}cm\)
Mặc khác: \({F_{ma{\rm{x}}}} = m{\omega ^2}A \Rightarrow \omega = \sqrt {\dfrac{{{F_{ma{\rm{x}}}}}}{{mA}}} = \sqrt {\dfrac{{0,4}}{{{{300.10}^{ - 3}}.\dfrac{{25}}{{12}}{{.10}^{ - 2}}}}} = 8rad/s\)
Một con lắc đơn có chu kỳ dao động điều hòa là \(T\). Khi giảm chiều dài con lắc \(10{\rm{ }}cm\) thì chu kỳ dao động của con lắc biến thiên \(0,1{\rm{ }}s\). Chu kỳ dao động \(T\) ban đầu của con lắc là:
Khi chiều dài của con lắc là l: \(T = 2\pi \sqrt {\dfrac{l}{g}} \)
Khi chiều dài của con lắc giảm \(10cm\) : \(T' = 2\pi \sqrt {\dfrac{{l - 0,1}}{g}} \)
Ta có: \(2\pi \sqrt {\dfrac{l}{g}} - 2\pi \sqrt {\dfrac{{l - 0,1}}{g}} = 0,1 \Rightarrow l = 1,08m \Rightarrow T = 2\pi \sqrt {\dfrac{l}{g}} = 2,06s\)
Động năng và thế năng của một vật dao động điều hoà với biên độ $A$ sẽ bằng nhau khi li độ của nó bằng :
Ta có:
\(\begin{array}{l}{{\rm{W}}_d} = {{\rm{W}}_t} \to {\rm{W}} = 2{W_t}\\ \leftrightarrow \dfrac{1}{2}k{A^2} = 2\dfrac{1}{2}k{x^2} \to x = \pm \dfrac{A}{{\sqrt 2 }}\end{array}\)
Trong các phương trình sau phương trình nào không biểu thị cho dao động điều hòa ?
Phương trình \(x = 3tsin(100\pi t + \frac{\pi }{6})\left( {cm} \right)\) không biểu thị cho dao động điều hòa vì biên độ trong phương trình này không phải là hằng số \(\left( {A = 3t} \right)\)
Một vật dao động điều hoà theo thời gian có phương trình \(x = Aco{s^2}(\pi t + \dfrac{\pi }{3})\) thì động năng và thế năng cũng dao động tuần hoàn với tần số góc:
\(x = Aco{s^2}(\omega t + \dfrac{\pi }{3}) = A\dfrac{{1 + cos\left( {2\omega t + \dfrac{{2\pi }}{3}} \right)}}{2} = \dfrac{A}{2} + \dfrac{A}{2}cos\left( {2\omega t + \dfrac{{2\pi }}{3}} \right)\)
=> Vật dao động điều hòa với tần số góc \(2\omega \)
=> Động năng và thế năng biến thiên tuần hoàn với tần số góc \(\omega ' = 2\left( {2\omega } \right) = 4\omega \)
Li độ của vật dao động điều hòa phụ thuộc vào thời gian theo quy luật sau:
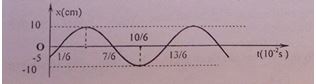
Phương trình dao động của vật là:
Từ đồ thị ta xác định được:
+ Biên độ dao động \(A{\rm{ }} = {\rm{ }}10{\rm{ }}cm\)
+ Thời gian ngắn nhất vật đi từ vị trí có li độ \(x{\rm{ }} = {\rm{ }} - {\rm{ }}5{\rm{ }}cm\) đến VTCB là \(\frac{{{{10}^{ - 2}}}}{6}s\)
\( \to \frac{T}{{12}} = \frac{{{{10}^{ - 2}}}}{6}\)
=> Chu kì dao động \(T{\rm{ }} = {\rm{ }}0,02{\rm{ }}s\)
=> Tần số góc \(\omega = \frac{{2\pi }}{T} = \frac{{2\pi }}{{0,02}} = 100\pi {\rm{ }}rad/s\)
+ Tại thời điểm \(t{\rm{ }} = {\rm{ }}0\) , vật đi qua vị trí \(x = - 5{\rm{ }}cm = \frac{{ - A}}{2}\) theo chiều dương
\( \to \left\{ \begin{array}{l}{x_0} = A\cos \varphi = - \frac{A}{2}\\v = - \omega A\sin \varphi > 0\end{array} \right. \to \varphi = - \frac{{2\pi }}{3}\)
Vậy phương trình dao động của vật là: \(x = 10cos\left( {100\pi t - \frac{{2\pi }}{3}} \right){\rm{ }}cm\)
Con lắc lò xo gồm vật nặng \(m{\rm{ }} = {\rm{ }}100g\) và lò xo nhẹ có độ cứng \(k{\rm{ }} = {\rm{ }}100N/m\). Tác dụng một ngoại lực cưỡng bức biến thiên điều hòa biên độ \({F_0}\) và tần số \({f_1} = {\rm{ }}6Hz\) thì biên độ dao động là \({A_1}\). Nếu giữ nguyên biên độ \({F_0}\) mà tăng tần số ngoại lực đến \({f_2} = {\rm{ }}5,5{\rm{ }}Hz\) thì biên độ dao động ổn định là \({A_2}\) . Kết luận đúng là:
Ta có:
+ Tần số dao động riêng của con lắc: \(f = \frac{1}{{2\pi }}\sqrt {\frac{k}{m}} = \frac{1}{{2\pi }}\sqrt {\frac{{100}}{{0,1}}} = 5H{\rm{z}}\)
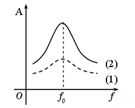
+ \({f_0} < {\rm{ }}{f_2} < {\rm{ }}{f_1}\)
\( \to {A_2} > {\rm{ }}{A_1}\)
Một vật thực hiện đồng thời ba dao động điều hoà cùng phương, cùng tần số có phương trình \({x_1} = 4c{\rm{os(10}}\pi {\rm{t + }}\dfrac{\pi }{4})cm\); \({x_2} = 4c{\rm{os(10}}\pi {\rm{t + }}\dfrac{{7\pi }}{{12}})cm\) và \({x_3} = 6\sin {\rm{(10}}\pi {\rm{t + }}\dfrac{\pi }{{12}})cm\). Phương trình dao động tổng hợp của vật là:
Dao động thành phần:
\({x_1} = 4cos(10\pi t + \dfrac{\pi }{4})(cm)\)
\({x_2} = 4cos(10\pi t + \dfrac{{7\pi }}{{12}})(cm)\)
\({x_3} = 6\sin (10\pi t + \dfrac{\pi }{{12}})(cm) = 6c{\rm{os}}(10\pi t - \dfrac{{5\pi }}{{12}})(cm)\)
Phương trình dao động tổng hợp \(x = {x_1} + {x_2} + {x_3}\)
Ta thấy: \({x_2},{x_3}\) dao động ngược pha nhau
Ta suy ra: \({x_{23}} = {x_2} + {x_3} = 2c{\rm{os}}\left( {10\pi t - \dfrac{{5\pi }}{{12}}} \right)cm\)
\( \to x = {x_1} + {x_{23}}\)
Độ lệch pha: \(\Delta \varphi = \dfrac{\pi }{4} + \dfrac{{5\pi }}{{12}} = \dfrac{{2\pi }}{3}(ra{\rm{d}})\)
+ Biên độ dao động tổng hợp:
\(\begin{array}{l}A = \sqrt {A_1^2 + A_{23}^2 + 2{A_1}{A_{23}}{\rm{cos}}\Delta \varphi } \\ = \sqrt {{4^2} + {2^2} + 2.4.2{\rm{cos}}\dfrac{{2\pi }}{3}} = 2\sqrt 3 cm\end{array}\)
+ Pha của dao động tổng hợp:
\(\begin{array}{l}\tan \varphi = \dfrac{{{A_1}\sin {\varphi _1} + {A_{23}}\sin {\varphi _{23}}}}{{{A_1}{\rm{cos}}{\varphi _1} + {A_{23}}{\rm{cos}}{\varphi _{23}}}}\\ = \dfrac{{4.\sin \frac{\pi }{4} + 2.\sin \dfrac{{ - 5\pi }}{{12}}}}{{{\rm{4}}{\rm{.cos}}\dfrac{\pi }{4} + 2{\rm{cos}}\dfrac{{ - 5\pi }}{{12}}}} = 2 - \sqrt 3 \\ \to \varphi = {15^0} = \dfrac{\pi }{{12}}\end{array}\)
=> Phương trình dao động tổng hợp: \(x = 2\sqrt 3 {\rm{cos}}\left( {10\pi t + \dfrac{\pi }{{12}}} \right)cm\)
Dao động tắt dần là dao động có:
Dao động tắt dần là dao động có biên độ giảm dần theo thời gian.
Khi nói về dao động cưỡng bức, phát biểu nào sau đây là đúng?
A - sai vì dao động của con lắc đồng hồ là dao động duy trì
B - sai vì biên độ của lực cưỡng bức F0 = Aω
C - đúng
D - sai vì dao động cưỡng bức có tần số bằng tần số của lực cưỡng bức

