Cho hai dao động điều hoà với li độ \({x_1}\) và \({x_2}\) có đồ thị như hình vẽ. Tổng tốc độ của hai dao động ở cùng một thời điểm có giá trị lớn nhất là:
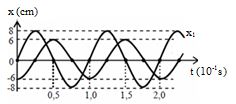
Từ đồ thị ta có: hai dao động đều có chu kì T = 0,1 s => \(\omega = 20\pi \) rad/s
Phương trình chất điểm 1 : là \({x_1} = 8\cos \left( {20\pi t - \frac{\pi }{2}} \right)cm\)
Phương trình chất điểm 2 là : \({x_2} = 6\cos \left( {20\pi t + \pi } \right)cm\)
Hai chất điểm vuông pha : \( \Rightarrow A = \sqrt {A_1^2 + A_2^2} = 10\)
Vận tốc lớn nhất : \({v_{m{\rm{ax}}}} = \omega .A = 20\pi .10 = 200\pi cm/s\)
Một con lắc dao động tắt dần trong môi trường với lực ma sát rất nhỏ. Cứ sau mỗi chu kì, phần năng lượng của con lăc bị mất đi \(6\% \). Trong một dao động toàn phần biên độ giảm đi bao nhiêu phần trăm?
Ta có: \(\dfrac{{\Delta W}}{{\rm{W}}} = \dfrac{{2\Delta A}}{A} = 6\% \to \dfrac{{\Delta A}}{A} = 3\% \)
Vậy trong một dao động toàn phần biên độ giảm đi \(3\% \)
Hai vật \({M_1}\) và \({M_2}\) dao động điều hòa cùng tần số. Hình bên là đồ thị biểu diễn sự phụ thuộc của li độ \(x\) của \({M_1}\) và vận tốc \({v_2}\) của \({M_2}\) theo thời gian t. Hai dao động của \({M_1}\) và \({M_2}\) lệch pha nhau:
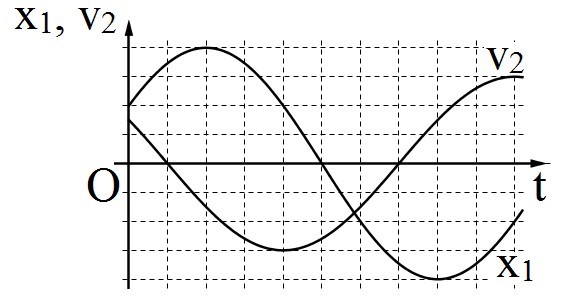
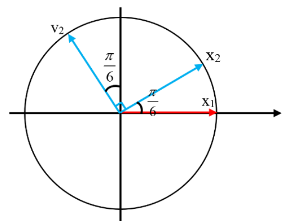
Từ đồ thị, ta có: \({v_2}\) nhanh pha hơn \({x_1}\) một góc \(\dfrac{{2\pi }}{3}\)
=> \({x_2}\) và \({x_1}\) lệch pha nhau một góc \(\dfrac{{2\pi }}{3} - \dfrac{\pi }{2} = \dfrac{\pi }{6}\)
Tiến hành thí nghiệm đo gia tốc trọng trường bằng con lắc đơn, một học sinh đo được chiều dài con lắc đơn là 119 ± 1 (cm), chu kì dao động nhỏ của nó là 2,20 ± 0,02 (s). Lấy π2 = 9,87 và bỏ qua sai số của số π. Gia tốc trọng trường do học sinh đo được tại nơi làm thí nghiệm là
Áp dụng công thức tính chu kì dao động:
\(T = 2\pi .\sqrt {\frac{l}{g}} \Rightarrow g = 4.{\pi ^2}.\frac{l}{{{T^2}}} = 4.9,87.\frac{{1,19}}{{2,{2^2}}} = 9,7068\left( {m/{s^2}} \right)\)
Công thức tính sai số:
\(\begin{array}{l}
\delta g = \delta l + 2.\delta T = \frac{1}{{119}} + \frac{{0,02}}{{2,2}} = 0,0175\\
\Rightarrow \Delta g = \overline g .\delta g = 9,7086.0,0175 = 0,17
\end{array}\)
Viết kết quả:
\(g = \overline g + \Delta g = 9,7086 \pm 0,17\left( {m/{s^2}} \right)\)
Một con lắc lò xo đang dao động điều hòa. Hình bên là đồ thị biểu diễn sự phụ thuộc của động năng \({{\rm{W}}_d}\) của con lắc theo thời gian \(t\). Biết \({t_3} - {t_2} = 0,25s\). Giá trị của \({t_4} - {t_1}\) là
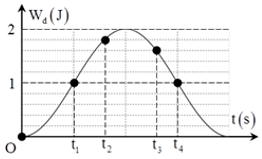
Xét đồ thị \({{\rm{W}}_d}' = {{\rm{W}}_d} - 1\left( J \right)\)
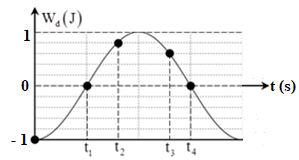
Từ đồ thị, ta có:
+ Tại \({t_1}\): \({{\rm{W}}_{{d_1}}}' = 0J\)
+ Tại \({t_2}:{{\rm{W}}_{{d_2}}}' = 0,8J\)
+ Tại \({t_3}:{{\rm{W}}_{{d_3}}}' = 0,6J\)
+ Tại \({t_4}:{{\rm{W}}_{{d_4}}} = 0J\)
Vẽ trên vòng tròn lượng giác, ta được:
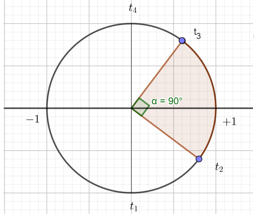
Ta có góc quét từ thời điểm \({t_2} \to {t_3}\) là \(\alpha = {90^0}\)
Lại có: \(\alpha = \omega '.\Delta t = \omega '\left( {{t_3} - {t_2}} \right)\)
\( \Rightarrow \omega ' = \dfrac{\alpha }{{{t_3} - {t_2}}} = \dfrac{{\dfrac{\pi }{2}}}{{0,25}} = 2\pi \left( {rad/s} \right)\)
Có góc quét từ thời điểm \({t_1} \to {t_4}\) là \(\Delta \varphi = \pi \)
Có: \(\Delta \varphi = \omega '\left( {{t_4} - {t_1}} \right) \Leftrightarrow \pi = 2\pi \left( {{t_4} - {t_1}} \right)\)
\( \Rightarrow {t_4} - {t_1} = \dfrac{1}{2}s\)
Một vật dao động điều hòa trên trục Ox. Hình bên là đồ thị biểu diễn sự phụ thuộc của li độ x vào thời gian t. Tần số góc của dao động là
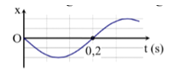
Từ đồ thị ta thấy \(\dfrac{T}{2} = 0,2s \Rightarrow T = 0,4s \Rightarrow \omega = \dfrac{{2\pi }}{T} = \dfrac{{2\pi }}{{0,4}} = 5\pi \,\,rad/s\)
Một con lắc lò xo nằm ngang gồm vật có khối lượng m = 100g, mang điện tích q = 4.10-4C được nối với lò xo cách điện có độ cứng k = 100N/m, đầu kia lò xo gắn vào điểm cố định. Buông nhẹ vật từ vị trí lò xo bị nén \(2\sqrt 3 cm\). Khi vật đi qua vị trí cân bằng lần đầu tiên thì bật một điện trường đều có cường độ E = 5000V/m dọc theo trục lò xo, cùng chiều vận tốc của vật. Sau đó vật dao động điều hòa với biên độ A1. Điện trường bật trong thời gian \(\frac{{31}}{{30}}\) giây thì tắt. Sau khi tắt điện trường, vật dao động điều hòa với biên độ A2. Biết trong quá trình sau đó lò xo luôn nằm trong giới hạn đàn hồi, lấy \({\pi ^2} = 10\). Bỏ qua ma sát giữa vật và sàn. Tỉ số \(\frac{{{A_2}}}{{{A_1}}}\) bằng:
Tần số góc của con lắc là: \(\omega = \sqrt {\dfrac{k}{m}} = \sqrt {\dfrac{{100}}{{0,1}}} = 10\sqrt {10} = 10\pi \,\,\left( {rad/s} \right)\)
Ban đầu khi chưa có điện trường, biên độ của con lắc là: \(A = 2\sqrt 3 \,\,\left( {cm} \right)\)
Tốc độ của vật khi ở VTCB khi đó là: \({v_{\max }} = \omega A = 10\pi .2\sqrt 3 = 20\pi \sqrt 3 \,\,\left( {cm/s} \right)\)
Khi có điện trường, VTCB của con lắc dịch chuyển một đoạn:
\(\Delta {\rm{l = }}\dfrac{{qE}}{k} = \dfrac{{{{4.10}^{ - 4}}.5000}}{{100}} = 0,02\,\,\left( m \right) = 2\,\,\left( {cm} \right)\)
Li độ của vật so với VTCB mới là: \(x = - 2\,\,\left( {cm} \right)\)
Ta có công thức độc lập với thời gian:
\({x^2} + \dfrac{{{v^2}}}{{{\omega ^2}}} = {A_1}^2 \Rightarrow {\left( { - 2} \right)^2} + \dfrac{{{{\left( {20\pi \sqrt 3 } \right)}^2}}}{{{{\left( {10\pi } \right)}^2}}} = {A_1}^2 \Rightarrow {A_1} = 4\,\,\left( {cm} \right)\)
Con lắc dao động trong thời gian \(\dfrac{{31}}{{30}}s\) trong điện trường, khi đó vecto quay được góc:
\(\Delta \varphi = \omega \Delta t = 10\pi .\dfrac{{31}}{{30}} = \dfrac{{31\pi }}{3} = 5.2\pi + \dfrac{\pi }{3}\,\,\left( {rad} \right)\)
Ta có vòng tròn lượng giác trong thời gian có điện trường:
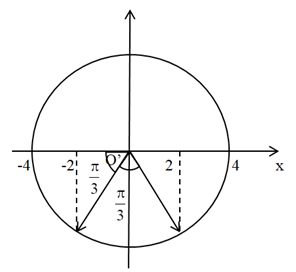
Từ vòng tròn lượng giác ta thấy tại thời điểm tắt điện trường, li độ của vật so với gốc O’ là:
\({x_1} = 4\cos \dfrac{\pi }{3} = 2\,\,\left( {cm} \right)\)
Áp dụng công thức độc lập với thời gian với gốc O’, ta có:
\({x_1}^2 + \dfrac{{{v^2}}}{{{\omega ^2}}} = {A_1}^2 \Rightarrow {2^2} + \dfrac{{{v^2}}}{{{{\left( {10\pi } \right)}^2}}} = {4^2} \Rightarrow \left| v \right| = 20\pi \sqrt 3 \,\,\left( {cm/s} \right)\)
Li độ của vật so với gốc O là: \({x_2} = {x_1} + OO' = 2 + 2 = 4\,\,\left( {cm} \right)\)
Áp dụng công thức độc lập với thời gian với gốc O, ta có:
\({x_2}^2 + \dfrac{{{v^2}}}{{{\omega ^2}}} = {A_2}^2 \Rightarrow {4^2} + \dfrac{{{{\left( {20\pi \sqrt 3 } \right)}^2}}}{{{{\left( {10\pi } \right)}^2}}} = {A_2}^2 \Rightarrow {A_2} = 2\sqrt 7 \,\,\left( {cm} \right)\)
Vậy tỉ số: \(\dfrac{{{A_2}}}{{{A_1}}} = \dfrac{{2\sqrt 7 }}{4} = \dfrac{{\sqrt 7 }}{2}\)
Con lắc lò xo lí tưởng được kích thích dao động điều hòa trên một mặt phẳng nghiêng góc \(\alpha \) như hình vẽ. Biết rằng gia tốc trọng trường tại nơi đặt con lắc là \(g\), tại vị trí cân bằng lò xo đã giãn một đoạn \(\Delta {l_0}\). Chu kì dao động \(T\) của con lắc được xác định bằng biểu thức
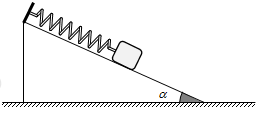
+ Chu kì dao động con lắc lò xo \(T = 2\pi \sqrt {\dfrac{m}{k}} \).
+ Tại vị trí cân bằng \(k\Delta {l_0} = mg\sin \alpha \Rightarrow \dfrac{m}{k} = \dfrac{{\Delta {l_0}}}{{g\sin \alpha }} \Rightarrow T = 2\pi \sqrt {\dfrac{{\Delta {l_0}}}{{g\sin \alpha }}} \)
Con lắc lò xo dao động điều hòa trên mặt phẳng nằm ngang với cơ năng là 0,2 J. Mốc tính thế năng ở vị trí cân bằng. Lấy \({{\pi }^{2}}=10.\) Khi lực đàn hồi của lò xo có độ lớn là \(\sqrt{2}\)N thì động năng bằng thế năng. Thời gian lò xo bị nén trong một chu kì là 0,5 s. Khi động lượng của vật là 0,157 kg.m/s thì tốc độ của vật bằng
Ta có: \(E=\frac{1}{2}k{{A}^{2}}=0,2(\text{J)}\) (1)
Theo đề bài: \(\left| {{F}_{dh}} \right|=\left| kx \right|=\sqrt{2}\) thì \({{\text{W}}_{d}}={{\text{W}}_{t}}\Leftrightarrow \left| x \right|=\frac{A}{\sqrt{2}}\)
\(\Rightarrow \) Fđhmax = kA = 2 (N) (2)
Từ (1), (2) \(\Rightarrow A=20\) (cm) hay \(k=10\)
Thời gian lò xo bị nén là: \({{t}_{n}}=\frac{T}{2}=0,\text{5 (s)}\Rightarrow \text{T}=\text{1 (s})\Rightarrow \omega =2\pi \)
\(\Rightarrow m=\frac{k}{{{\omega }^{2}}}=0,25(kg)\)
\(\Rightarrow v=\frac{p}{m}=0,628(m/s)=62,8(m/s)\)
Một vật thực hiện đồng thời hai dao động điều hòa cùng phương, cùng tần số có dạng \({x_1} = {A_1}\cos 10t\) và \({x_2} = {A_2}\cos \left( {10t + {\varphi _2}} \right)\). Biết phương trình dao động tổng hợp là \(x = {A_1}\sqrt 3 \cos \left( {10t + \varphi } \right)\), trong đó \({\varphi _2} - \varphi = \dfrac{\pi }{6}\). Xác định tỉ số \(\dfrac{\varphi }{{{\varphi _2}}}\)
Ta có giản đồ vecto:

Từ giản đồ vecto, ta có định lí hàm sin:
\(\dfrac{{{A_1}}}{{\sin \dfrac{\pi }{6}}} = \dfrac{{{A_1}\sqrt 3 }}{{\sin \alpha }} \Rightarrow \sin \alpha = \dfrac{{\sqrt 3 }}{2} \Rightarrow \left[ \begin{array}{l}\alpha = \dfrac{{2\pi }}{3}\,\,\left( {rad} \right)\\\alpha = \dfrac{\pi }{3}\,\,\left( {rad} \right)\end{array} \right.\)
Với \(\alpha = \dfrac{{2\pi }}{3} \Rightarrow \varphi = \pi - \left( {\dfrac{\pi }{6} + \dfrac{{2\pi }}{3}} \right) = \dfrac{\pi }{6}\,\,\left( {rad} \right)\)
\( \Rightarrow {\varphi _2} = \varphi + \dfrac{\pi }{6} = \dfrac{\pi }{6} + \dfrac{\pi }{6} = \dfrac{\pi }{3}\,\,\left( {rad} \right) \Rightarrow \dfrac{\varphi }{{{\varphi _2}}} = \dfrac{{\dfrac{\pi }{6}}}{{\dfrac{\pi }{3}}} = \dfrac{1}{2}\)
Với \(\alpha = \dfrac{\pi }{3} \Rightarrow \varphi = \pi - \left( {\dfrac{\pi }{6} + \dfrac{\pi }{3}} \right) = \dfrac{\pi }{2}\,\,\left( {rad} \right)\)
\( \Rightarrow {\varphi _2} = \varphi + \dfrac{\pi }{6} = \dfrac{\pi }{2} + \dfrac{\pi }{6} = \dfrac{{2\pi }}{3}\,\,\left( {rad} \right) \Rightarrow \dfrac{\varphi }{{{\varphi _2}}} = \dfrac{{\dfrac{\pi }{2}}}{{\dfrac{{2\pi }}{3}}} = \dfrac{3}{4}\)

