Câu hỏi:
2 năm trước
Một con lắc lò xo đang dao động điều hòa. Hình bên là đồ thị biểu diễn sự phụ thuộc của động năng \({{\rm{W}}_d}\) của con lắc theo thời gian \(t\). Biết \({t_3} - {t_2} = 0,25s\). Giá trị của \({t_4} - {t_1}\) là
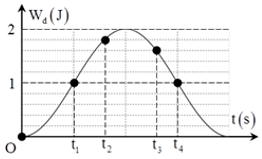
Trả lời bởi giáo viên
Đáp án đúng: b
Xét đồ thị \({{\rm{W}}_d}' = {{\rm{W}}_d} - 1\left( J \right)\)
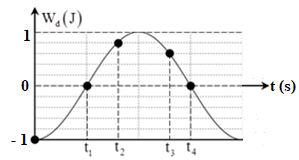
Từ đồ thị, ta có:
+ Tại \({t_1}\): \({{\rm{W}}_{{d_1}}}' = 0J\)
+ Tại \({t_2}:{{\rm{W}}_{{d_2}}}' = 0,8J\)
+ Tại \({t_3}:{{\rm{W}}_{{d_3}}}' = 0,6J\)
+ Tại \({t_4}:{{\rm{W}}_{{d_4}}} = 0J\)
Vẽ trên vòng tròn lượng giác, ta được:
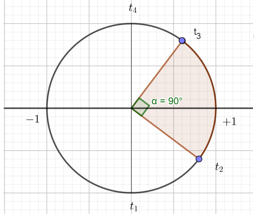
Ta có góc quét từ thời điểm \({t_2} \to {t_3}\) là \(\alpha = {90^0}\)
Lại có: \(\alpha = \omega '.\Delta t = \omega '\left( {{t_3} - {t_2}} \right)\)
\( \Rightarrow \omega ' = \dfrac{\alpha }{{{t_3} - {t_2}}} = \dfrac{{\dfrac{\pi }{2}}}{{0,25}} = 2\pi \left( {rad/s} \right)\)
Có góc quét từ thời điểm \({t_1} \to {t_4}\) là \(\Delta \varphi = \pi \)
Có: \(\Delta \varphi = \omega '\left( {{t_4} - {t_1}} \right) \Leftrightarrow \pi = 2\pi \left( {{t_4} - {t_1}} \right)\)
\( \Rightarrow {t_4} - {t_1} = \dfrac{1}{2}s\)
Hướng dẫn giải:
+ Đọc đồ thị
+ Sử dụng công thức tính góc quét: \(\Delta \varphi = \omega \Delta t\)
+ Sử dụng vòng tròn lượng giác
Câu hỏi khác
- Bài tập xác định thời gian vật chuyển động từ x1 đến x2, số lần qua li độ x có lời giải MÔN LÝ lớp 12
- Bài tập lí thuyết dao động điều hòa có lời giải MÔN LÝ lớp 12
- Bài tập các đại lượng đặc trưng của DĐĐH có lời giải MÔN LÝ lớp 12
- Bài tập xác định quãng đường, tốc độ trung bình của vật trong DĐĐH có lời giải MÔN LÝ lớp 12
- Bài tập viết phương trình dao động điều hòa có lời giải MÔN LÝ lớp 12
