Một con lắc lò xo nằm ngang gồm vật có khối lượng m = 100g, mang điện tích q = 4.10^-4C được nối với lò xo cách điện có độ cứng k = 100N/m, đầu kia lò xo gắn vào điểm cố định. Buông nhẹ vật từ vị trí lò xo bị nén \(2\sqrt 3 cm\). Khi vật đi qua vị trí cân bằng lần đầu tiên thì bật một điện trường đều có cường độ E = 5000V/m dọc theo trục lò xo, cùng chiều vận tốc của vật. Sau đó vật dao động điều hòa với biên độ A₁. Điện trường bật trong thời gian \(\frac{{31}}{{30}}\) giây thì tắt. Sau khi tắt điện trường, vật dao động điều hòa với biên độ A₂. Biết trong quá trình sau đó lò xo luôn nằm trong giới hạn đàn hồi, lấy \({\pi ^2} = 10\). Bỏ qua ma sát giữa vật và sàn. Tỉ số \(\frac{{{A_2}}}{{{A_1}}}\) bằng:

Tần số góc của con lắc là: \(\omega  = \sqrt {\dfrac{k}{m}}  = \sqrt {\dfrac{{100}}{{0,1}}}  = 10\sqrt {10}  = 10\pi \,\,\left( {rad/s} \right)\)

Ban đầu khi chưa có điện trường, biên độ của con lắc là: \(A = 2\sqrt 3 \,\,\left( {cm} \right)\)

Tốc độ của vật khi ở VTCB khi đó là: \({v_{\max }} = \omega A = 10\pi .2\sqrt 3  = 20\pi \sqrt 3 \,\,\left( {cm/s} \right)\)

Khi có điện trường, VTCB của con lắc dịch chuyển một đoạn:

\(\Delta {\rm{l = }}\dfrac{{qE}}{k} = \dfrac{{{{4.10}^{ - 4}}.5000}}{{100}} = 0,02\,\,\left( m \right) = 2\,\,\left( {cm} \right)\)

Li độ của vật so với VTCB mới là: \(x =  - 2\,\,\left( {cm} \right)\)

Ta có công thức độc lập với thời gian:

\({x^2} + \dfrac{{{v^2}}}{{{\omega ^2}}} = {A_1}^2 \Rightarrow {\left( { - 2} \right)^2} + \dfrac{{{{\left( {20\pi \sqrt 3 } \right)}^2}}}{{{{\left( {10\pi } \right)}^2}}} = {A_1}^2 \Rightarrow {A_1} = 4\,\,\left( {cm} \right)\)

Con lắc dao động trong thời gian \(\dfrac{{31}}{{30}}s\) trong điện trường, khi đó vecto quay được góc:

\(\Delta \varphi  = \omega \Delta t = 10\pi .\dfrac{{31}}{{30}} = \dfrac{{31\pi }}{3} = 5.2\pi  + \dfrac{\pi }{3}\,\,\left( {rad} \right)\)

Ta có vòng tròn lượng giác trong thời gian có điện trường:

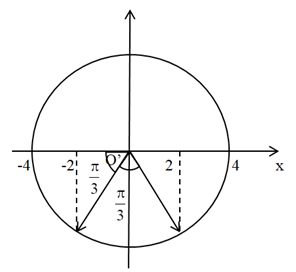
Từ vòng tròn lượng giác ta thấy tại thời điểm tắt điện trường, li độ của vật so với gốc O’ là:

\({x_1} = 4\cos \dfrac{\pi }{3} = 2\,\,\left( {cm} \right)\)

Áp dụng công thức độc lập với thời gian với gốc O’, ta có:

\({x_1}^2 + \dfrac{{{v^2}}}{{{\omega ^2}}} = {A_1}^2 \Rightarrow {2^2} + \dfrac{{{v^2}}}{{{{\left( {10\pi } \right)}^2}}} = {4^2} \Rightarrow \left| v \right| = 20\pi \sqrt 3 \,\,\left( {cm/s} \right)\)

Li độ của vật so với gốc O là: \({x_2} = {x_1} + OO' = 2 + 2 = 4\,\,\left( {cm} \right)\)

Áp dụng công thức độc lập với thời gian với gốc O, ta có:

\({x_2}^2 + \dfrac{{{v^2}}}{{{\omega ^2}}} = {A_2}^2 \Rightarrow {4^2} + \dfrac{{{{\left( {20\pi \sqrt 3 } \right)}^2}}}{{{{\left( {10\pi } \right)}^2}}} = {A_2}^2 \Rightarrow {A_2} = 2\sqrt 7 \,\,\left( {cm} \right)\)

Vậy tỉ số: \(\dfrac{{{A_2}}}{{{A_1}}} = \dfrac{{2\sqrt 7 }}{4} = \dfrac{{\sqrt 7 }}{2}\)