Câu hỏi:
2 năm trước
Li độ của vật dao động điều hòa phụ thuộc vào thời gian theo quy luật sau:
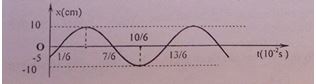
Phương trình dao động của vật là:
Trả lời bởi giáo viên
Đáp án đúng: b
Từ đồ thị ta xác định được:
+ Biên độ dao động \(A{\rm{ }} = {\rm{ }}10{\rm{ }}cm\)
+ Thời gian ngắn nhất vật đi từ vị trí có li độ \(x{\rm{ }} = {\rm{ }} - {\rm{ }}5{\rm{ }}cm\) đến VTCB là \(\frac{{{{10}^{ - 2}}}}{6}s\)
\( \to \frac{T}{{12}} = \frac{{{{10}^{ - 2}}}}{6}\)
=> Chu kì dao động \(T{\rm{ }} = {\rm{ }}0,02{\rm{ }}s\)
=> Tần số góc \(\omega = \frac{{2\pi }}{T} = \frac{{2\pi }}{{0,02}} = 100\pi {\rm{ }}rad/s\)
+ Tại thời điểm \(t{\rm{ }} = {\rm{ }}0\) , vật đi qua vị trí \(x = - 5{\rm{ }}cm = \frac{{ - A}}{2}\) theo chiều dương
\( \to \left\{ \begin{array}{l}{x_0} = A\cos \varphi = - \frac{A}{2}\\v = - \omega A\sin \varphi > 0\end{array} \right. \to \varphi = - \frac{{2\pi }}{3}\)
Vậy phương trình dao động của vật là: \(x = 10cos\left( {100\pi t - \frac{{2\pi }}{3}} \right){\rm{ }}cm\)
Hướng dẫn giải:
Sử dụng kĩ năng đọc đồ thị dao động
+ Xác định biên độ dao động
+ Xác định chu kì => tần số góc: \(\omega = \frac{{2\pi }}{T}\)
+ Xác định tại \(t = 0:\left\{ \begin{array}{l}x = A\cos \varphi \\v = - A\omega \sin \varphi \end{array} \right.\)
Câu hỏi khác
- Bài tập xác định thời gian vật chuyển động từ x1 đến x2, số lần qua li độ x có lời giải MÔN LÝ lớp 12
- Bài tập lí thuyết dao động điều hòa có lời giải MÔN LÝ lớp 12
- Bài tập các đại lượng đặc trưng của DĐĐH có lời giải MÔN LÝ lớp 12
- Bài tập xác định quãng đường, tốc độ trung bình của vật trong DĐĐH có lời giải MÔN LÝ lớp 12
- Bài tập viết phương trình dao động điều hòa có lời giải MÔN LÝ lớp 12
