Dùng prôtôn bắn vào hạt nhân \({}_{\rm{4}}^{\rm{9}}{\rm{Be}}\) đứng yên, sau phản ứng sinh ra hạt α và hạt nhân X có động năng lần lượt là K_α = 3,575 MeV và K_X = 3,150 MeV. Phản ứng này tỏa ra năng lượng bằng  ΔE = 2,125 MeV. Coi khối lượng các hạt nhân tỉ lệ với số khối của nó. Góc hợp giữa các hướng chuyển động của hạt α và hạt prôtôn là

+ Phương trình phản ứng: \({}_0^1p + {}_4^9Be \to {}_2^4\alpha  + {}_2^6X\)  

+ Năng lượng toả ra của phản ứng hạt nhân: ∆E = K_α + K_X – K_p = 2,125

=> K_p = 4,6 MeV

+ Áp dụng định luật bảo toàn động lượng: \(\overrightarrow {{p_p}}  = \overrightarrow {{p_X}}  + \overrightarrow {{p_\alpha }} \)

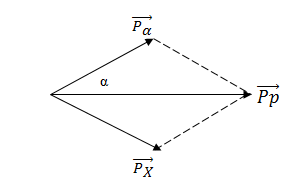
Áp dụng định lí hàm số cos ta có: \(p_X^2 = p_p^2 + p_\alpha ^2 - 2{p_p}{p_\alpha }c{\rm{os}}\alpha \)

\(\begin{array}{l}{p^2} = 2mK\\ \Rightarrow 2{m_X}{K_X} = 2{m_p}{K_p} + 2m{K_\alpha } - 4\sqrt {{m_p}{K_p}{m_a}{K_\alpha }} cos\alpha \\ \Leftrightarrow {m_X}{K_X} = {m_p}{K_p} + {m_\alpha }{K_\alpha } - 2\sqrt {{m_p}{K_p}{m_a}{K_\alpha }} cos\alpha \\ \Leftrightarrow 6.3,150 = 1.4,6 + 4.3,575 - 2\sqrt {1.4,6.4.3,575} cos\alpha \\ \Rightarrow cos\alpha  = 0\\ \Rightarrow \alpha  = {90^0}\end{array}\)