Câu hỏi:
2 năm trước
Bắn một hạt proton với vận tốc \({3.10^7}m/s\) đến va chạm với hạt nhân Li đang đứng yên, gây ra phản ứng hạt nhân. Sau phản ứng tạo thành hai hạt nhân giống nhau chuyển động với cùng vận tốc, bay theo hai hướng tạo với nhau góc \({160^0}\). Coi khối lượng của các hạt gần đúng là số khối (với đơn vị u). Biết \(1u{c^2} = 931,5MeV\). Năng lượng tỏa ra là:
Trả lời bởi giáo viên
Đáp án đúng: c
Phương trình phản ứng: \(p + {}_3^7Li \to {}_2^4X + {}_2^4X\)
Ta có, khối lượng của proton \({m_p} = {A_p} = 1u\) , vận tốc của proton \(v = {3.10^7}m/s = 0,1c\) (\(c = {3.10^8}m/s\) vận tốc ánh sáng)
Động năng của proton \({K_P} = \dfrac{1}{2}m{v^2} = \dfrac{1}{2}u.{\left( {0,1c} \right)^2} = \dfrac{1}{2}0,{1^2}.931,5 = 4,6575MeV\)
Theo bảo toàn động lượng: \({\vec p_p} = {\vec p_{X_1}} + {\vec p_{X_2}}\)
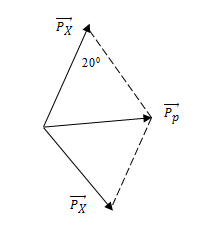
\(P_p^2 = P_X^2 + P_X^2 - 2{P_X}{P_X}c{\rm{os}}{20^0} \Rightarrow {K_p} = {m_X}{K_X} + {m_X}{K_X} - 2{m_X}{K_X}\cos ({20^0}) \Rightarrow {K_X} = 9,653MeV\)
Năng lượng tỏa ra là \(\Delta E = 2{K_X} - {K_p} = 14,6MeV\)
Hướng dẫn giải:
+ Áp dụng định luật bảo toàn động lượng trong phản ứng hạt nhân
+ Công thức liên hệ giữa động năng và động lượng: p2 = 2mK
+ Công thức tính năng lượng toả ra của phản ứng: \(\Delta E = {K_s} - {K_t}\)
(Ks, Kt lần lượt là tổng động năng của các hạt sau và tổng động năng của các hạt trước phản ứng)
+ Định lí hàm số cos trong tam giác
Câu hỏi khác
- Bài tập năng lượng liên kết, năng lượng liên kết riêng có lời giải MÔN LÝ lớp 12
- Bài tập tính chất và cấu tạo hạt nhân - bài tập cấu tạo hạt nhân nguyên tử lý 12 có lời giải
- Bài tập phản ứng hạt nhân lý 12 có lời giải
- Bài tập phóng xạ - lí thuyết chung lý 12 có lời giải
- Bài tập phản ứng hạt nhân - bài tập xác định động năng, vận tốc, góc của các hạt lý 12 có lời giải
