Một hạt \(\alpha \) có động năng \(3,9{\rm{ }}MeV\) đến đập vào hạt nhân \(_{13}^{27}Al\) đứng yên gây nên phản ứng hạt nhân \(\alpha + _{13}^{27}Al \to n + _{15}^{30}P\). Tính tổng động năng của các hạt sau phản ứng. Cho \({m_\alpha } = {\rm{ }}4,0015u\); \({\rm{ }}{m_n} = {\rm{ }}1,0087u\); \({\rm{ }}{m_{Al}} = {\rm{ }}26,97345u\) ;\({\rm{ }}{m_p} = {\rm{ }}29,97005u\) ; \({\rm{ }}1u{c^2} = {\rm{ }}931{\rm{ }}MeV\)
- Cách 1:
Ta có: \(\Delta E = \left( {{m_\alpha } + {m_{Al}} - {m_n} - {m_p}} \right){c^2} = - 3,5378(MeV)\)
\(\to {{\rm{W}}_d}_{_n} + {{\rm{W}}_{{d_P}}} = \Delta E + {{\rm{W}}_{{d_\alpha }}} = - 3,5378 + 3,9 = 0,3622{\rm{ }}MeV\)
- Cách 2:
Áp dụng định luật bảo toàn năng lượng toàn phần, ta có:
\(\begin{array}{l}{{\rm{W}}_{{d_\alpha }}} + \left( {{m_\alpha } + {m_{Al}}} \right){c^2} = \left( {{m_n} + {m_p}} \right){c^2} + {{\rm{W}}_{{d_n}}} + {{\rm{W}}_{{d_p}}}\\ \to {{\rm{W}}_{{d_n}}} + {{\rm{W}}_{{d_p}}} = {{\rm{W}}_{{d_\alpha }}} + ({m_\alpha } + {m_{Al}} - {m_n} - {m_p}){c^2} = 3,9 - 3,5378 = 0,3622MeV\end{array}\)
Hạt \(\alpha \) có động năng \(6,3{\rm{ }}MeV\) bắn vào một hạt nhân \(_4^9Be\) đứng yên, gây ra phản ứng \(\alpha + _4^9Be \to _6^{12}C + n\). Cho biết phản ứng tỏa ra một năng lượng \(5,7{\rm{ }}MeV\) , động năng của hạt C gấp 5 lần động năng hạt n. Động năng của hạt nhân n là
Áp dụng định luật bảo toàn năng lượng, ta có:
\(\left\{ \begin{array}{l}{{\rm{W}}_{{d_C}}}{\rm{ + }}{W_{{d_n}}} = \Delta E + {{\rm{W}}_{{d_\alpha }}} = 5,7 + 6,3 = 12(MeV)\\{{\rm{W}}_{{d_C}}} = 5{W_{{d_n}}}\end{array} \right. \to \left\{ \begin{array}{l}{{\rm{W}}_{{d_C}}} = \left( {{{\rm{W}}_{{d_\alpha }}} + \Delta E} \right)\frac{5}{{5 + 1}} = 12.\frac{5}{6} = 10(MeV)\\{W_{{d_n}}} = \left( {{{\rm{W}}_{{d_\alpha }}} + \Delta E} \right)\frac{1}{{5 + 1}} = 12.\frac{1}{6} = 2(MeV)\end{array} \right.\)
Dùng hạt proton có động năng 1,6 MeV bắn vào hạt nhân Liti (\(_3^7Li\) ) đứng yên. Giả sử sau phản ứng thu được hai hạt giống nhau có cùng động năng và không kèm theo tia \(\gamma \). Biết năng lượng tỏa ra của phản ứng là 17,4 MeV. Động năng của mỗi hạt sinh ra là:
Gọi hạt nhân tạo thành sau phản ứng là X
Ta có:
\(\begin{array}{l}{\rm{2}}{W_{{d_X}}} = \Delta E + {{\rm{W}}_{{d_\alpha }}} = 17,4 + 1,6 = 19(MeV)\\ \to {W_{{d_X}}} = \frac{{19}}{2} = 9,5(MeV)\end{array}\)
Cho hạt proton có động năng 1,2 MeV bắn phá hạt nhân \(_3^7Li\)đang đứng yên tạo ra 2 hạt nhân X giống nhau nhưng tốc độ chuyển động thì gấp đôi nhau. Cho biết phản ứng tỏa ra một năng lượng 17,4 MeV và không sinh ra bức xạ \(\gamma \) . Động năng của hạt nhân X có tốc độ lớn hơn là:
\({v_{{X_1}}} = {\rm{ }}2{v_{{X_2}}} \to {{\rm{W}}_{{d_{{X_1}}}}} = 4{{\rm{W}}_{{d_{{X_2}}}}}\)
\(\begin{array}{l}\left\{ \begin{array}{l}{{\rm{W}}_{{d_{{X_1}}}}}{\rm{ + }}{{\rm{W}}_{{d_{{X_2}}}}} = \Delta E + {{\rm{W}}_{{d_p}}} = 17,4 + 1,2 = 18,6(MeV)\\{{\rm{W}}_{{d_{{X_1}}}}} = 4{{\rm{W}}_{{d_{{X_2}}}}}\end{array} \right.\\ \to \left\{ \begin{array}{l}{{\rm{W}}_{{d_{X2}}}} = \left( {{{\rm{W}}_{{d_p}}} + \Delta E} \right)\frac{4}{{4 + 1}} = 18,6.\frac{4}{5} = 14,88(MeV)\\{{\rm{W}}_{{d_{X1}}}} = \left( {{{\rm{W}}_{{d_p}}} + \Delta E} \right)\frac{1}{{4 + 1}} = 18,6.\frac{1}{5} = 3,72(MeV)\end{array} \right.\end{array}\)
Hạt A có động năng WA bắn vào một hạt nhân B đứng yên, gây ra phản ứng: \(A{\rm{ }} + {\rm{ }}B \to C{\rm{ }} + {\rm{ }}D\) . Hai hạt sinh ra có cùng độ lớn vận tốc và khối lượng lần lượt là mC và mD. Cho biết tổng năng lượng nghỉ của các hạt trước phản ứng nhiều hơn tổng năng lượng nghỉ của các hạt sau phản ứng là \(\Delta E\) và không sinh ra bức xạ \(\gamma \) . Tính động năng của hạt nhân C.
\(A{\rm{ }} + {\rm{ }}B \to C{\rm{ }} + {\rm{ }}D\)
\({v_C} = {v_D} \to \frac{{{{\rm{W}}_{{d_C}}}}}{{{{\rm{W}}_{{d_D}}}}} = \frac{{{m_C}{v_C}^2}}{{{m_D}{v_D}^2}} = \frac{{{m_C}}}{{{m_D}}}\)
Mặt khác: \({{\rm{W}}_C} + {{\rm{W}}_D} = {{\rm{W}}_A} + \Delta E\)
\({{\rm{W}}_{{d_C}}} = \left( {{{\rm{W}}_A} + \Delta E} \right)\frac{{{m_C}}}{{{m_C} + {m_D}}}\)
Bắn hạt α vào hạt nhân \(_7^{14}N\) đứng yên có phản ứng \(_7^{14}N + \alpha \to _8^{17}O + _1^1p\) . Các hạt sinh ra có cùng véctơ vận tốc. Cho khối lượng hạt nhân (đo bằng đơn vị u) xấp xỉ bằng số khối của nó. Tỉ số tốc độ của hạt nhân Oxi và tốc độ của hạt \(\alpha \) là:
\(_7^{14}N + \alpha \to _8^{17}O + _1^1p\)
Ta có: \(\overrightarrow {{v_O}} = \overrightarrow {{v_p}} \)
Áp dụng định luật bảo toàn động lượng:
\({P_s}{\rm{ \;}} \leftrightarrow {m_\alpha }\overrightarrow {{v_\alpha }} {\rm{ \;}} = {m_O}\overrightarrow {{v_O}} {\rm{ \;}} + {m_p}\overrightarrow {{v_p}} \)
\(\overrightarrow {{v_O}} {\rm{ \;}} = \overrightarrow {{v_p}} {\rm{ \;}} \to {m_\alpha }{v_\alpha }{\rm{ \;}} = \left( {{m_O} + {m_p}} \right){v_O} \to {v_O}{\rm{ \;}} = {v_p}{\rm{\;}} = \dfrac{{{m_\alpha }{v_\alpha }}}{{{m_O} + {m_p}}} = \dfrac{4}{{17 + 1}}{v_\alpha }{\rm{ \;}} = \dfrac{2}{9}{v_\alpha }{\rm{ }}\)
Bắn hạt α vào hạt nhân \(_7^{14}N\) đứng yên, xảy ra phản ứng tạo thành một hạt nhân oxi và một hạt proton. Biết rằng hai hạt sinh ra có véctơ vận tốc như nhau, phản ứng thu năng lượng 1,21 MeV. Cho khối lượng của các hạt nhân thỏa mãn: \({m_O}{m_\alpha } = {\rm{ }}0,21{\left( {{m_O} + {m_P}} \right)^2}\) và \({m_p}{m_\alpha } = 0,012{\left( {{m_O} + {m_P}} \right)^2}\). Động năng của hạt α là:
\(_7^{14}N + \alpha \to _8^{17}O + _1^1p\)
Ta có: \(\overrightarrow {{v_O}} = \overrightarrow {{v_p}} \)
Áp dụng định luật bảo toàn động lượng: \(\overrightarrow {{P_t}} = \overrightarrow {{P_s}} \leftrightarrow {m_\alpha }\overrightarrow {{v_\alpha }} = {m_O}\overrightarrow {{v_O}} + {m_p}\overrightarrow {{v_p}} \)
\(\begin{array}{l}\overrightarrow {{v_O}} = \overrightarrow {{v_p}} \to {m_\alpha }\overrightarrow {{v_\alpha }} = \left( {{m_O} + {m_p}} \right)\overrightarrow {{v_O}} \\ \to \overrightarrow {{v_O}} = \overrightarrow {{v_p}} = \frac{{{m_\alpha }\overrightarrow {{v_\alpha }} }}{{{m_O} + {m_p}}}\end{array}\)
\(\left\{ \begin{array}{l}{{\rm{W}}_O} = \frac{1}{2}{m_O}v_O^2\\{{\rm{W}}_p} = \frac{1}{2}{m_p}v_p^2\end{array} \right. \to \left\{ \begin{array}{l}{{\rm{W}}_O} = \frac{{{m_O}{m_\alpha }}}{{{{\left( {{m_O} + {m_p}} \right)}^2}}}{{\rm{W}}_\alpha }\\{{\rm{W}}_p} = \frac{{{m_p}{m_\alpha }}}{{{{\left( {{m_O} + {m_p}} \right)}^2}}}{{\rm{W}}_\alpha }\end{array} \right. \to \left\{ \begin{array}{l}{{\rm{W}}_O} = 0,21{{\rm{W}}_\alpha }\\{{\rm{W}}_p} = 0,012{W_\alpha }\end{array} \right.\)
Mặt khác,
\(\begin{array}{l}\Delta E + {{\rm{W}}_\alpha } = {{\rm{W}}_O} + {{\rm{W}}_p}\\ \to \Delta E = {{\rm{W}}_O} + {{\rm{W}}_p} - {{\rm{W}}_\alpha } \leftrightarrow - 1,21 = 0,21{{\rm{W}}_\alpha } + 0,012{{\rm{W}}_\alpha } - {{\rm{W}}_\alpha }\\ \to {{\rm{W}}_\alpha } = 1,555(MeV)\end{array}\)
Phản ứng hạt nhân \(_1^2H + _1^3H \to _2^4He + _0^1n\) tỏa ra năng lượng 17,6 MeV. Giả sử ban đầu động năng các hạt không đáng kể. Coi khối lượng các hạt nhân (theo u) xấp xỉ số khối của nó. Động năng của \(_0^1n\) là:
Ta có:
\(\begin{array}{l}\overrightarrow 0 = {m_\alpha }\overrightarrow {{v_\alpha }} + {m_n}\overrightarrow {{v_n}} \to {m_\alpha }\overrightarrow {{v_\alpha }} = - {m_n}\overrightarrow {{v_n}} \\ \to {\left( {{m_\alpha }\overrightarrow {{v_\alpha }} } \right)^2} = {\left( { - {m_n}\overrightarrow {{v_n}} } \right)^2} \to {m_\alpha }{{\rm{W}}_\alpha } = {m_n}{{\rm{W}}_n}\\ \to {{\rm{W}}_\alpha } = \frac{1}{4}{{\rm{W}}_n}\end{array}\)
Mặt khác: \(\Delta E = {{\rm{W}}_\alpha } + {{\rm{W}}_n} = \frac{1}{4}{{\rm{W}}_n} + {{\rm{W}}_n} \to {{\rm{W}}_n} = \frac{{17,6}}{{1,25}} = 14,08(MeV)\)
Hạt nhân \(\alpha \) có động năng \(5,3{\rm{ }}MeV\) bắn phá hạt nhân \(_4^9Be\) đứng yên và gây ra phản ứng: \(\alpha + _4^9Be \to X + n\). Hai hạt sinh ra có phương véctơ vận tốc vuông góc với nhau. Cho biết tổng năng lượng nghỉ của các hạt trước phản ứng nhiều hơn tổng năng lượng nghỉ của các hạt sau phản ứng là \(5,6791{\rm{ }}MeV\) , khối lượng của các hạt \({m_\alpha } = {\rm{ }}3,968{m_n};{\rm{ }}{m_X} = {\rm{ }}11,8965{m_n}\) . Động năng của hạt X là:
\(\alpha + _4^9Be \to X + n\)
Ta có: \(\widehat {\overrightarrow {{v_X}} ,\overrightarrow {{v_n}} } = {90^0}\)
\(\begin{array}{l}\overrightarrow {{v_X}} \bot \overrightarrow {{v_n}} \to \left\{ \begin{array}{l}P_\alpha ^2 = P_X^2 + P_n^2\\{{\rm{W}}_{{d_\alpha }}} + \Delta E = {{\rm{W}}_{{d_X}}} + {{\rm{W}}_{{d_n}}}\end{array} \right. \to \left\{ \begin{array}{l}{m_\alpha }{{\rm{W}}_{{d_\alpha }}} = {m_X}{{\rm{W}}_{{d_X}}} + {m_n}{{\rm{W}}_{{d_n}}}\\{{\rm{W}}_{{d_\alpha }}} + \Delta E = {{\rm{W}}_{{d_X}}} + {{\rm{W}}_{{d_n}}}\end{array} \right.\\ \to \left\{ \begin{array}{l}3,968{m_n}.5,3 = 11,8965{m_n}{{\rm{W}}_{{d_X}}} + {m_n}{{\rm{W}}_{{d_n}}}\\5,3 + 5,6791 = {{\rm{W}}_{{d_X}}} + {{\rm{W}}_{{d_n}}}\end{array} \right. \to \left\{ \begin{array}{l}{{\rm{W}}_X} = 0,922(MeV)\\{{\rm{W}}_n} = 10,06(MeV)\end{array} \right.\end{array}\)
Dùng một proton có động năng 5,45 MeV bắn vào hạt nhân \(_4^9Be\) đang đứng yên. Phản ứng tạo ra hạt nhân X và hạt α. Hạt α bay ra theo phương vuông góc với phương tới của proton và có động năng 4 MeV. Khi tính động năng của các hạt, lấy khối lượng của các hạt tính theo đơn vị khối lượng nguyên tử bằng số khối của chúng. Năng lượng tỏa ra trong các phản ưng này bằng:
\(_1^1p + _4^9Be \to _2^4\alpha + _3^6X\)
Ta có: \(\widehat {\overrightarrow {{v_\alpha }} ,\overrightarrow {{v_p}} } = {90^0}\)
\(\begin{array}{l}\overrightarrow {{v_\alpha }} \bot \overrightarrow {{v_p}} \to \left\{ \begin{array}{l}P_X^2 = P_\alpha ^2 + P_p^2\\{{\rm{W}}_{{d_p}}} + \Delta E = {{\rm{W}}_{{d_X}}} + {{\rm{W}}_{{d_\alpha }}}\end{array} \right. \to \left\{ \begin{array}{l}{m_X}{{\rm{W}}_{{d_X}}} = {m_\alpha }{{\rm{W}}_{{d_\alpha }}} + {m_p}{{\rm{W}}_{{d_p}}}\\{{\rm{W}}_{{d_p}}} + \Delta E = {{\rm{W}}_{{d_X}}} + {{\rm{W}}_{{d_\alpha }}}\end{array} \right.\\ \to \left\{ \begin{array}{l}6.{{\rm{W}}_{{d_X}}} = 4.4 + 1.5,45\\\Delta E = {{\rm{W}}_{{d_X}}} + {{\rm{W}}_{{d_\alpha }}} - {{\rm{W}}_{{d_p}}}\end{array} \right. \to \left\{ \begin{array}{l}{{\rm{W}}_X} = 3,575(MeV)\\\Delta E = 3,575 + 4 - 5,45 = 2,125(MeV)\end{array} \right.\end{array}\)
Bắn phá một proton vào hạt nhân \(_3^7Li\)đứng yên. Phản ứng hạt nhân sinh ra hai hạt nhân X giống nhau và có cùng tốc độ. Biết tốc độ của proton bằng 4 lần tốc độ của hạt nhân X. Coi khối lượng của các hạt nhân bằng số khối theo đơn vị u. Góc tạo bởi phương chuyển động của hai hạt X là:
\(_1^1p + _3^7Be \to _2^4{X_1} + _2^4{X_2}\)
Áp dụng định luật bảo toàn động lượng, ta có:
\(\begin{array}{l}{m_p}\overrightarrow {{v_p}} = {m_X}\overrightarrow {{v_{{X_1}}}} + {m_X}\overrightarrow {{v_{{X_2}}}} \\ \to {\left( {{m_p}{v_p}} \right)^2} = \left[ {{{\left( {{m_X}{v_{{X_1}}}} \right)}^2} + {{\left( {{m_X}{v_{{X_2}}}} \right)}^2} + 2{m_X}{v_{{X_1}}}{m_X}{v_{{X_2}}}{\rm{cos}}\varphi } \right]\\ \leftrightarrow {\left( {{m_p}{v_p}} \right)^2} = 2{\left( {{m_X}{v_{{X_1}}}} \right)^2} + 2{\left( {{m_X}{v_{{X_1}}}} \right)^2}{\rm{cos}}\varphi \end{array}\)
với \(\varphi = \widehat {\overrightarrow {{v_{{X_1}}}} ;\overrightarrow {{v_{{X_2}}}} }\)
\(\begin{array}{l} \to {\rm{cos}}\varphi = \frac{{{{\left( {{m_p}{v_p}} \right)}^2}}}{{2{{\left( {{m_X}{v_{{X_1}}}} \right)}^2}}} - 1 = \frac{{{{(1.4{v_X})}^2}}}{{2{{(4.{v_X})}^2}}} - 1 = - \frac{1}{2}\\ \to \varphi = {120^0}\end{array}\)
Hạt α có động năng 5 MeV bắn vào một hạt nhân \(_4^9Be\) đứng yên, gây ra phản ứng tạo thành một hạt \(_6^{12}C\) và một hạt nơtron. Hai hạt sinh ra có véctơ vận tốc hợp với nhau một góc 800. Cho biết phản ứng tỏa ra một năng lượng 5,6 MeV. Coi khối lượng của các hạt nhân bằng số khối theo đơn vị u. Động năng của hạt nhân C có thể bằng
Phương trình phản ứng: \(_2^4\alpha + _4^9Be \to _6^{12}C + _0^1n\)
Hai hạt sinh ra có véctơ vận tốc hợp với nhau góc 800, ta có:
\(\begin{array}{l}P_\alpha ^2 = P_C^2 + P_n^2 + 2{P_C}{P_n}{\rm{cos}}{80^0}\\ \leftrightarrow {m_\alpha }{{\rm{W}}_{{d_\alpha }}} = {m_C}{{\rm{W}}_{{d_C}}} + {m_n}{{\rm{W}}_{{d_n}}} + 2\sqrt {{m_C}{{\rm{W}}_{{d_C}}}} \sqrt {{m_n}{{\rm{W}}_{{d_n}}}} {\rm{cos}}{80^0}\\ \leftrightarrow 4.5 = 12{{\rm{W}}_{{d_C}}} + {{\rm{W}}_n} + 2\sqrt {12.{{\rm{W}}_{{d_C}}}} \sqrt {{{\rm{W}}_{{d_n}}}} {\rm{cos}}{80^0}{\rm{ (1)}}\end{array}\)
Mặt khác, ta có:
\(\begin{array}{l}{{\rm{W}}_{{d_\alpha }}} + \Delta E = {{\rm{W}}_{{d_C}}} + {{\rm{W}}_{{d_n}}}\\ \leftrightarrow 5 + 5,6 = {{\rm{W}}_{{d_C}}} + {{\rm{W}}_{{d_n}}}\\ \to {{\rm{W}}_{{d_n}}} = 10,6 - {{\rm{W}}_{{d_C}}}{\rm{ (2)}}\end{array}\)
Thế (2) vào (1), ta được:
\(\begin{array}{l}4.5 = 12{{\rm{W}}_{{d_C}}} + (10,6 - {{\rm{W}}_{{d_C}}}) + 2\sqrt {12.{{\rm{W}}_{{d_C}}}} \sqrt {(10,6 - {{\rm{W}}_{{d_C}}})} {\rm{cos}}{80^0}\\ \leftrightarrow {\rm{11}}{{\rm{W}}_{{d_C}}} + 2c{\rm{os8}}{{\rm{0}}^0}\sqrt {12{{\rm{W}}_{{d_C}}}(10,6 - {{\rm{W}}_{{d_C}}})} = 9,4\\ \leftrightarrow \left\{ \begin{array}{l}{{\rm{W}}_{{d_C}}} \le 10,6\\{\left( {2c{\rm{os8}}{{\rm{0}}^0}} \right)^2}12{{\rm{W}}_{{d_C}}}(10,6 - {{\rm{W}}_{{d_C}}}) = {\left( {9,4 - {\rm{11}}{{\rm{W}}_{{d_C}}}} \right)^2}\end{array} \right.\\ \to \left\{ \begin{array}{l}{{\rm{W}}_{{d_C}}} \le 10,6\\\left[ \begin{array}{l}{{\rm{W}}_{{d_C}}} = 1,225(MeV)\\{{\rm{W}}_{{d_C}}} = 0,589(MeV)\end{array} \right.\end{array} \right.\end{array}\)
Dùng chùm proton bắn phá hạt nhân \(_3^7Li\) đang đứng yên tạo ra 2 hạt nhân X giống nhau có cùng động năng là \(W\) nhưng bay theo hai hướng hợp với nhau một góc \(\varphi \) và không sinh ra tia gamma. Biết tổng năng lượng nghỉ của các hạt trước phản ứng chuyển nhiều hơn tổng năng lượng nghỉ của các hạt tạo thành là \(2W/3\). Coi khối lượng hạt nhân đo bằng đơn bị khối lượng nguyên tử gần bằng số khối của nó thì:
Phương trình: \(p + _3^7Li \to _2^4X + _2^4X\)
Ta có: \({{\rm{W}}_{{d_p}}} + \Delta E = 2{{\rm{W}}_{{d_X}}} \to {{\rm{W}}_{{d_p}}} = 2{{\rm{W}}_{{d_X}}} - \Delta E = 2{\rm{W}} - \dfrac{2}{3}{\rm{W = }}\dfrac{4}{3}{\rm{W}}\)
Mặt khác: \(\widehat {\overrightarrow {{v_X}} ,\overrightarrow {{v_X}} } = \varphi \)
\(\begin{array}{l}P_p^2 = P_X^2 + P_X^2 + 2{P_X}{P_X}{\rm{cos}}\varphi \\ \leftrightarrow {m_p}{{\rm{W}}_{{d_p}}} = 2{m_X}{{\rm{W}}_{{d_X}}} + 2{m_X}{{\rm{W}}_{{d_X}}}{\rm{cos}}\varphi \\ \leftrightarrow \dfrac{4}{3}{\rm{W}} = 2.4{\rm{W}}(1 + c{\rm{os}}\varphi {\rm{)}} \to c{\rm{os}}\varphi = - \dfrac{5}{6}\end{array}\)
Hạt nơtron có động năng 2 MeV bắn vào hạt nhân \(_3^7Li\) đứng yên, gây ra phản ứng hạt nhân tạo thành một hạt α và một hạt T. Các hạt α và T bay theo các hướng hợp với hướng tới của hạt notrơn những góc tương ứng bằng 150 và 300. Bỏ qua bức xạ gamma. Phản ứng thu hay tỏa năng lương? ( Cho tỉ số giữa các khối lượng hạt nhân bằng tỉ số giữa các số khối của chúng)
\(_0^1n + _3^7Li \to _2^4\alpha + _1^4T\)
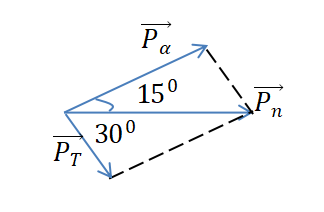
Từ hình, ta có:
\(\begin{array}{l}\dfrac{{{P_\alpha }}}{{\sin {{30}^0}}} = \dfrac{{{P_T}}}{{\sin {{15}^0}}} = \dfrac{{{P_n}}}{{\sin ({{180}^0} - {{30}^0} - {{15}^0})}}\\ \leftrightarrow \dfrac{{{m_\alpha }{v_\alpha }}}{{\sin {{30}^0}}} = \dfrac{{{m_T}{v_T}}}{{\sin {{15}^0}}} = \dfrac{{{m_n}{v_n}}}{{\sin {{135}^0}}}\\ \leftrightarrow \dfrac{{\sqrt {2{m_\alpha }{{\rm{W}}_{d\alpha }}} }}{{\sin {{30}^0}}} = \dfrac{{\sqrt {2{m_T}{{\rm{W}}_{dT}}} }}{{\sin {{15}^0}}} = \dfrac{{\sqrt {2{m_n}{{\rm{W}}_{dn}}} }}{{\sin {{135}^0}}}\\ \to \left\{ \begin{array}{l}{{\rm{W}}_{d\alpha }} = \dfrac{{{m_n}{{\rm{W}}_{dn}}}}{{{m_\alpha }}}{\left( {\dfrac{{\sin {{30}^0}}}{{\sin {{135}^0}}}} \right)^2} = \dfrac{{1.2}}{4}\frac{1}{2} = 0,25(MeV)\\{{\rm{W}}_{dT}} = \dfrac{{{m_n}{{\rm{W}}_{dn}}}}{{{m_T}}}{\left( {\dfrac{{\sin {{15}^0}}}{{\sin {{135}^0}}}} \right)^2} = \dfrac{{1.2}}{4}\dfrac{{2 - \sqrt 3 }}{2} = 0,067(MeV)\end{array} \right.\end{array}\)
Mặt khác:
\(\begin{array}{l}{{\rm{W}}_n} + \Delta E = {{\rm{W}}_\alpha } + {{\rm{W}}_T}\\ \to \Delta E = {{\rm{W}}_\alpha } + {{\rm{W}}_T} - {{\rm{W}}_n} = 0,25 + 0,067 - 4 = - 1,683(MeV)\end{array}\)
Bắn một proton vào hạt nhân \(_3^7Li\)đứng yên. Phản ứng tạo ra hai hạt nhân X giống nhau bay cùng tốc độ và theo các phương hợp với phương tới của proton các góc bằng nhau là 600. Lấy khối lượng của mỗi hạt nhân tính theo đơn vị u bằng số khối của nó. Tỉ số giữa tốc độ của proton và tốc độ của hạt nhân X là
Ta có:
\(_1^1p + _3^7Li \to _2^4X + _2^4X\)
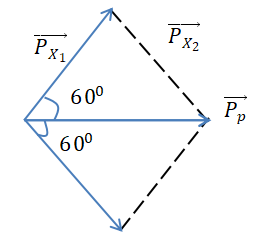
Từ hình, ta suy ra:
\(\begin{array}{l}{P_p} = {P_X} \leftrightarrow {m_p}{v_p} = {m_X}{v_X}\\ \to \dfrac{{{v_p}}}{{{v_X}}} = \dfrac{{{m_X}}}{{{m_p}}} = \dfrac{4}{1} = 4\end{array}\)

