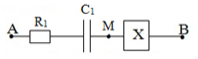
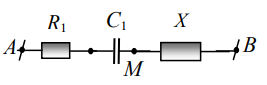
Đặt điện áp \(u = 220\sqrt 2 \cos \left( {100\pi t + \varphi } \right)\,\,\left( V \right)\) vào hai đầu đoạn mạch AB như hình bên. Biết hộp X là đoạn mạch có R, L, C mắc nối tiếp; cường độ dòng điện hiệu dụng trong mạch là \(2\sqrt 2 \,\,A\) và \({R_1} = 20\sqrt 2 \,\,\Omega \). Tại thời điểm t (s) cường độ dòng điện trong mạch bằng 4 A. Đến thời điểm \(t + \frac{1}{{300}}\,\,\left( s \right)\) thì điện áp u = 0 và đang giảm. Công suất của đoạn mạch X là
và \({R_1} = 20\sqrt 2 \,\,\Omega \). Tại thời điểm t (s) cường độ dòng điện trong mạch bằng 4 A. Đến thời điểm \(t + \frac{1}{{300}}\,\,\left( s \right)\) thì điện áp u = 0 và đang giảm. Công suất của đoạn mạch X là
Trả lời bởi giáo viên
Hai thời điểm lệch pha nhau là:
\(\Delta \varphi = \omega \Delta t = 100\pi .\frac{1}{{300}} = \frac{\pi }{3}\,\,\left( {rad} \right)\)
Ở thời điểm t, cường độ dòng điện trong mạch: I = 4 (A) = I0
Ta có vòng tròn lượng giác:
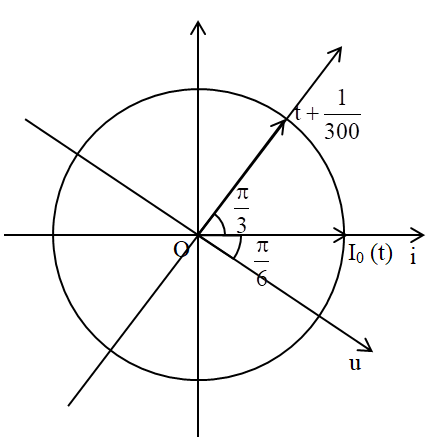
Tại thời điểm \(t + \frac{1}{{300}}s\), điện áp giữa hai đầu đoạn mạch bằng 0 và đang giảm
→ trục u lệch pha \(\frac{\pi }{6}\) so với trục i \( \Rightarrow \varphi = \frac{\pi }{6}\)
Công suất tiêu thụ của đoạn mạch là:
\(P = UI\cos \varphi = 220.2\sqrt 2 .cos\frac{\pi }{6} = 538,9\,\,\left( {\rm{W}} \right)\)
Công suất tiêu thụ của đoạn mạch X là:
\({P_X} = P - {I^2}{R_1} = 538,9 - {\left( {2\sqrt 2 } \right)^2}.20\sqrt 2 = 312,6\,\,\left( {\rm{W}} \right)\)
Hướng dẫn giải:
Sử dụng vòng tròn lượng giác và công thức: ∆φ = ω.∆t
Công suất của mạch điện: P = UIcosφ