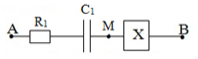
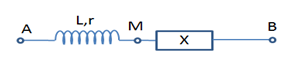
Cho mạch điện như hình vẽ. Đặt vào hai đầu đoạn \(AB\) một điện áp xoay chiều có chu kì \(T\), lúc đó \({Z_L} = \sqrt 3 r\). Hộp X chứa 2 trong ba phần tử điện trở \(R\), tụ điện có dung kháng \({Z_C}\), cuộn thuần cảm có độ tự cảm \({Z_{{L_0}}}\) ghép nối tiếp. Biết vào thời điểm \({t_1}\) thì điện áp tức thời \({u_{AM}}\) cực đại, đến thời điểm \(t = {t_1} + \dfrac{T}{3}\) thì điện áp tức thời \({u_{MB}}\) cực đại. Hộp X chứa các phần tử là
Trả lời bởi giáo viên
Ta có giản đồ vecto:
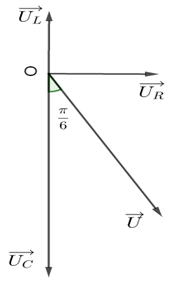
Ta có \(t = {t_1} + \dfrac{T}{3}\) nên \({U_{AM}}\) sớm pha góc \({120^0}\) so với \({U_{MB}}\)
Lệch pha nhau góc \({120^0}\) mà tại AM có \({Z_L} = \sqrt 3 r \Rightarrow {Z_L}\) lệch pha \({60^0}\) so với \(r\)
Nên \(AM\) sớm pha \({60^0}\) so với dòng điện.
Suy ra MB chậm pha \({120^0} - {60^0} = {60^0}\) so với dòng điện.
\( \Rightarrow X\) là R nối tiếp với C
\(\tan \left( { - {{60}^0}} \right) = \dfrac{{ - {Z_C}}}{R} \Rightarrow {Z_C} = \sqrt 3 R\)
Hướng dẫn giải:
Vận dụng độ lệch pha của các phần tử