Sóng có tần số \(16Hz\) truyền trên chất lỏng với tốc độ \(200cm/s\), gây ra các dao động theo phương thẳng đứng của các phần tử chất lỏng. Hai điểm M và N thuộc mặt chất lỏng cùng phương truyền sóng cách nhau \(21,875cm\). Biết điểm M nằm gần nguồn sóng hơn. Tại thời điểm t điểm N hạ xuống thấp nhất. Hỏi sau đó thời gian ngắn nhất là bao nhiêu thì điểm M sẽ hạ xuống thấp nhất?
Trả lời bởi giáo viên
Ta có: \(\lambda = \dfrac{v}{f} = \dfrac{{200}}{{16}} = 12,5cm\)
Chu kì: \(T = \dfrac{1}{f} = \dfrac{1}{{16}}{\rm{s}}\)
Độ lệch pha giữa hai điểm M và N là: \(\Delta \varphi = \dfrac{{2\pi \Delta d}}{\lambda } = \dfrac{{2\pi .21,875}}{{12,5}} = \dfrac{{7\pi }}{2} = 2\pi + \dfrac{{3\pi }}{2}\)
=> M và N dao động vuông pha nhau
Vì M gần nguồn sóng hơn => M nhanh pha hơn N 1 góc \(\dfrac{{3\pi }}{2}\)
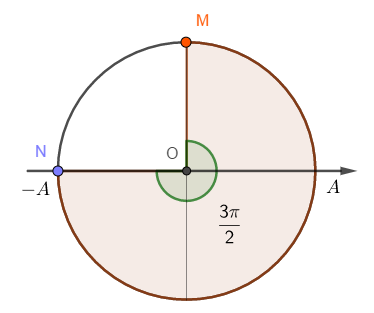
Tại thời điểm t: N đang ở biên âm, M đang ở VTCB theo chiều âm
=> Thời gian ngắn nhất điểm M hạ xuống thấp nhất (biên âm) là: \(\Delta t = \dfrac{T}{4} = \dfrac{{\dfrac{1}{{16}}}}{4} = \dfrac{1}{{64}}s\)
Hướng dẫn giải:
+ Áp dụng công thức tính bước sóng: \(\lambda = \dfrac{v}{f}\)
+ Áp dụng công thức tính chu kì: \(T = \dfrac{1}{f} = 0,05{\rm{s}}\)
+ Vận dụng công thức tính độ lệch pha: \(\Delta \varphi = \dfrac{{2\pi \Delta d}}{\lambda }\)
+ Sử dụng vòng tròn lượng giác.

