Một sợi dây đàn hồi có chiều dài \(l = 60cm\) và hai đầu dây cố định. Khi được kích thích dao động, trên dây hình thành sóng dừng với \(4\) bó sóng và biên độ dao động tại bụng là \(4cm\). Tại M gần nguồn phát sóng tới (tại A) nhất có biên độ dao động là \(2\sqrt 3 cm\). Đoạn MA dài:
Trả lời bởi giáo viên
Sử dụng điều kiện để có sóng dừng với trường hợp 2 đầu dây cố định \(l = k\frac{\lambda }{2}\) , trong đó k là só bó sóng. Mà óng dừng trong trường hợp trên có 4 bó sóng nên \(k{\rm{ }} = {\rm{ }}4\) nên ta có \(l = k\dfrac{\lambda }{2} \Leftrightarrow 60 = 4.\dfrac{\lambda }{2} \Leftrightarrow \lambda = 30cm\)
Bụng sóng dao động với biên độ là: \(2a{\text{ }} = {\text{ }}4cm \to a{\text{ }} = {\text{ }}2cm\)
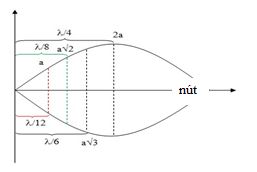
Điểm M dao động với biên độ \(2\sqrt 3 = a\sqrt 3 \) nên M sẽ cách điểm nút gần nó nhất một khoảng là \(\dfrac{\lambda }{6} = \dfrac{{30}}{6} = 5cm\)
Hướng dẫn giải:
Sử dụng lí thuyết về điều kiện có sóng dừng trên dây hai đầu cố định: $l = k\dfrac{\lambda }{2}$

