Trong hiện tượng giao thoa sóng nước hai nguồn kết hợp A, B cách nhau một khoảng \(a = 20cm\) dao động điều hòa theo phương thẳng đứng, cùng pha, cùng tần số \(50{\rm{ }}Hz\). Tốc độ truyền sóng trên mặt nước là \(1,5{\rm{ }}m/s\). Xét các điểm trên mặt nước thuộc đường tròn tâm A, bán kính AB, điểm nằm trên đường tròn dao động với biên độ cực đại cách đường trung trực của AB gần nhất một khoảng:
Trả lời bởi giáo viên
Để M là cực đại và gần trung trực của AB nhất thì M phải nằm trên hypebol ứng với \(k = 1\)
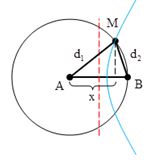
+ Ta có:
\({d_1} - {d_2} = \lambda {k} = 17cm\)
\(\begin{array}{l}\left\{ \begin{array}{l}{h^2} = {20^2} - {x^2}\\{h^2} = {17^2} - {\left( {20 - x} \right)^2}\end{array} \right.\\ \Rightarrow {20^2} - {x^2} = {17^2} - {\left( {20 - x} \right)^2}\\ \Rightarrow x = 12,775cm\end{array}\)
Vậy khoảng cách từ M đến trung trực sẽ là \(2,775{\rm{ }}cm\)
Hướng dẫn giải:
Điều kiện để có cực đại giao thoa trong giao thoa sóng hai nguồn cùng pha: \({d_2} - {d_1} = k\lambda \)

