Trên một sợi dây đàn hồi đang có sóng dừng ổn định. Ba điểm \(M,{\rm{ }}N,{\rm{ }}P\) là ba điểm liên tiếp trên dây dao động với cùng biên độ \(4{\rm{ }}cm\), biết M, N dao động cùng pha, \(N,{\rm{ }}P\) dao động ngược pha. Khi các điểm qua vị trị cân bằng khoảng cách \(MN{\rm{ }} = {\rm{ }}2NP{\rm{ }} = {\rm{ }}20{\rm{ }}cm\). Biên độ của bụng sóng và bước sóng:
Trả lời bởi giáo viên
Theo đề bài ta vẽ được hình dạng sóng dừng như bên:
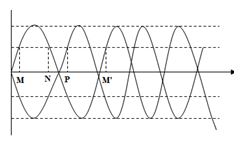
Từ \(M\) đến \(M'\) là một bước sóng.
Dựa vào hình vẽ tính được
\(\lambda = MM' = 2\left( {MN + NP} \right) = 60cm\)
\(P\) là điểm gần nút sóng nhất có biên độ \(4cm\), cách nút sóng một đoạn bằng \(\dfrac{{NP}}{2} = 5cm\) . Ta có:
\({A_P} = 2A\left| {\cos \left( {\dfrac{{2\pi .d}}{\lambda } + \dfrac{\pi }{2}} \right)} \right| = 2A\left| {\cos \left( {\dfrac{{2\pi .5}}{{60}} + \dfrac{\pi }{2}} \right)} \right| = 4cm \Rightarrow A = 4cm\)
Vậy biên độ bụng sóng là \(2A = 8cm\)
Hướng dẫn giải:
Áp dụng công thức tính biên độ sóng dừng: \(A = 2a\left| {\cos \left( {\dfrac{{2\pi d}}{\lambda } + \dfrac{\pi }{2}} \right)} \right| = 2a\left| {\sin \left( {\dfrac{{2\pi d}}{\lambda }} \right)} \right|\)

