Tại vị trí $O$ trên mặt đất có một nguồn âm điểm phát âm đẳng hướng ra không gian với công suất không đổi. Hai điểm $P$ và $Q$ lần lượt trên mặt đất sao cho $OP$ vuông góc với $OQ$. Một thiết bị xác định mức cường độ âm $M$ bắt đầu chuyển động thẳng với gia tốc $a$ không đổi từ $P$ hướng đến $Q$, sau khoảng thời gian $t_1$ thì $M$ đo được mức cường độ âm lớn nhất; tiếp đó $M$ chuyển động thẳng đều và sau khoảng thời gian \(0,125{t_1}\) thì đến điểm $Q$. Mức cường độ âm đo được tại $P$ là \(20{\rm{ }}dB\). Mức cường độ âm tại $Q$ mà máy đo được là:
Trả lời bởi giáo viên
+ Ta có hình vẽ sau
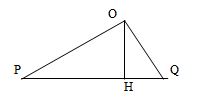
+ Sau khoảng thời gian \({t_1}\) thì $M$ đo được mức cường độ âm lớn nhất => máy đi được quãng đường \(PH = \dfrac{{at_1^2}}{2}\), và vận tốc của máy tại H là \(v = a{t_1}\)
+ Sau đó vật chuyển động thẳng đều và đi được quãng đường HQ trong thời gian \(0,125{t_1}\)
=>\(HQ = v.t =a{t_1}.0,125{t_1} = 0,125at_1^2\)
=> Cạnh huyền \(PQ = PH + HQ = 0,625at_1^2\)
+ Theo hệ thức lượng trong tam giác vuông ta có
\(OP = \sqrt {PH.PQ} = \sqrt {0,5.0,625} at_1^2\) ; \(OQ = \sqrt {HQ.PQ} = \sqrt {0,125.0,625} at_1^2\)
Ta có \({L_Q} - {L_P} = 10log\dfrac{{O{P^2}}}{{O{Q^2}}} = 10log\dfrac{{0,5.0,625}}{{0,125.0,625}} = 6\)
\( \to {L_Q}{\rm{ = }}{L_P} + 6 = 26dB\)
Hướng dẫn giải:
+ Sử dụng lí thuyết về sóng âm,
kết hợp với tính chất của chuyển động thẳng biến đổi đều và chuyển động thẳng đều
+ Sử dụng biểu thức quãng đường đi trong chuyển động biến đổi đều: \(s = \dfrac{1}{2}a{t^2}\)
+ Sử dụng biểu thức quãng đường đi trong chuyển động thẳng đều: \(s = vt\)
+ Vận dụng công thức tính mức cường độ âm và hiệu mức cường độ âm: \(\left\{ \begin{array}{l}L = 10\log \dfrac{I}{{{I_0}}}\left( {dB} \right)\\{L_A} - {L_B} = 10\log \dfrac{{{I_A}}}{{{I_B}}} = 10\log \dfrac{{r_B^2}}{{r_A^2}}\end{array} \right.\)

