Một vận động viên hằng ngày đạp xe trên đoạn đường thẳng từ điểm \(A\) đúng lúc còi báo thức bắt đầu kêu, khi đến điểm \(B\) thì còi vừa dứt. Mức cường độ âm tại \(A\) và \(B\) lần lượt là \(60{\rm{ }}dB\) và \(54{\rm{ }}dB\). Còi đặt tại \(O\), phát âm đẳng hướng với công suất không đổi và môi trường không hấp thụ âm; góc \(AOB\) bằng \({150^0}\) . Biết rằng vận động viên này khiếm thính nên chỉ nghe được mức cường độ âm từ \(66{\rm{ }}dB\) trở lên và tốc độ đạp xe không đổi, thời gian còi báo thức kêu là \(1\) phút. Trên đoạn đường \(AB\), vận động viên nghe thấy tiềng còi báo thức trong khoảng thời gian xấp xỉ bằng:
Trả lời bởi giáo viên
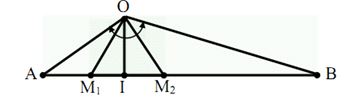
Tai của người người khiếm thính nghe được khi người đó đi từ M1 đến M2
\(\left\{ \begin{gathered}
\underbrace {{L_A} - {L_B}}_{0,6} = \log \dfrac{{O{B^2}}}{{O{A^2}}} \hfill \\
\underbrace {{L_M} - {L_A}}_{0,6} = \log \dfrac{{O{A^2}}}{{OM_1^2}} \hfill \\
\end{gathered} \right. \Rightarrow \left\{ \begin{gathered}
\dfrac{{O{B^2}}}{{O{A^2}}} = {10^{0,6}} \hfill \\
\dfrac{{O{A^2}}}{{OM_1^2}} = {10^{0,6}} \hfill \\
\end{gathered} \right.\xrightarrow{{OA = 1}}\left\{ \begin{gathered}
O{B^2} = {10^{0,6}} \hfill \\
O{M^2} = {10^{ - 0,6}} \hfill \\
\end{gathered} \right. \Rightarrow \left\{ \begin{gathered}
OB = {10^{0,3}} \hfill \\
OM = {10^{ - 0,3}} \hfill \\
\end{gathered} \right.\)
\(\left\{ \begin{array}{l}AB = \sqrt {O{A^2} + O{B^2} - 2OA.OB\cos {{150}^0}} \approx 2,90\\{S_{\Delta OAB}} = \dfrac{1}{2}AB.OI = \dfrac{1}{2}OA.OB\sin {150^0} \Rightarrow OI \approx 0,34\end{array} \right.\)
\(0,5{M_1}{M_2} = \sqrt {OM_1^2 - O{I^2}} \approx 0,37 \Rightarrow {M_1}{M_2} \approx 0,74\)
\(\left\{ \begin{array}{l}AB = v.t\\{M_1}{M_2} = v.{t_1}\end{array} \right. \Rightarrow {t_1} = \dfrac{{{M_1}{M_2}}}{{AB}}.t = \dfrac{{0,74}}{{2,90}}.60 \approx 15s\)
Hướng dẫn giải:
+ Sử dụng công thức tính cường độ âm và mức cường độ âm:\(I = \dfrac{P}{{4\pi {r^2}}};L = 10\log \dfrac{I}{{{I_0}}}(dB)\)
+ Sử dụng biểu thức hiệu mức cường độ âm: \({L_A} - {L_B} = 10\log \dfrac{{{I_A}}}{{{I_B}}} = 10\log \dfrac{{r_B^2}}{{r_A^2}}\)
+ Sử dụng công thức tính diện tích tam giác: \(S = \dfrac{1}{2}ah\)

