Cho \(4\) điểm \(O,{\rm{ }}M,{\rm{ }}N\) và \(P\) đồng phẳng, nằm trong một môi trường truyền âm. Trong đó, \(M\) và \(N\) nằm trên nửa đường thẳng xuất phát từ \(O\), tam giác \(MNP\) là tam giác đều. Tại \(O\), đặt một nguồn âm điểm có công suất không đổi, phát âm đẳng hướng ra môi trường. Coi môi trường không hấp thụ âm. Biết mức cường độ âm tại \(M\) và \(N\) lần lượt là \(50dB\) và \(40dB\). Mức cường độ âm tại \(P\) là:
Trả lời bởi giáo viên
Theo đề bài ta có hình vẽ sau:
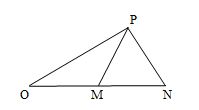
\({L_M} = {\text{ }}50dB,{\text{ }}{L_N} = {\text{ }}40dB\)
\(\begin{array}{l} \to {L_M} - {L_N} = 10\log \dfrac{{r_N^2}}{{r_M^2}} = 10\\ \to \dfrac{{r_N^2}}{{r_M^2}} = {10^1} \Rightarrow {r_N} = \sqrt {10} {r_M}\end{array}\)
Tam giác $MNP$ là tam giác đều cạnh $a$
=> \({r_N} = {\rm{ }}{r_M} + {\rm{ }}a\)
=> \({r_M} = \dfrac{a}{{\sqrt {10} - 1}};{r_N} = \dfrac{{a\sqrt {10} }}{{\sqrt {10} - 1}}\)
Áp dụng định lí hàm số sin trong tam giác $OPN$ ta có:
\(\begin{array}{l}O{P^2} = \sqrt {O{N^2} + P{N^2} - 2ON.PN.cos\widehat {ONP}} \\ \Leftrightarrow {r_P} = \sqrt {r_N^2 + {a^2} - 2.{r_N}.a.cos{{60}^0}} \\ = a\sqrt {{{\left( {\dfrac{{\sqrt {10} }}{{\sqrt {10} - 1}}} \right)}^2} + 1 - 2.\dfrac{{\sqrt {10} }}{{\sqrt {10} - 1}}.1.\dfrac{1}{2}} \approx 1,295a\end{array}\)
Khi đó
\(\begin{array}{l}{L_M} - {L_P} = 10\log \dfrac{{r_P^2}}{{r_M^2}} = 10\log \dfrac{{{{1,295}^2}}}{{{{\left( {\dfrac{1}{{\sqrt {10} - 1}}} \right)}^2}}} \approx 8,94\\ \Rightarrow {L_P} = {L_M} - 8,94 = 50 - 8,94 = 41,06dB \approx 41,1dB\end{array}\)
Hướng dẫn giải:
Sử dụng biểu thức hiệu mức cường độ âm: \({L_A} - {L_B} = 10\log \dfrac{{{I_A}}}{{{I_B}}} = 10\log \dfrac{{r_B^2}}{{r_A^2}}\)

