Trên bề mặt chất lỏng cho hai nguồn sóng \({O_1},{O_2}\) cách nhau \(24cm\) có phương trình lần lượt \({u_1} = {\rm{ }}{u_2} = 6cos(40\pi t - \dfrac{\pi }{2}){\rm{ }}\left( {mm} \right)\). Cho tốc độ truyền sóng trên bề mặt chất lỏng \(80\left( {cm/s} \right)\). Tại thời điểm t sóng từ nguồn \({O_1}\) vừa truyền tới trung điểm của đoạn thẳng \({O_1}{O_2}\). Xét phần tử phần tử \(M\)có vị trí cân bằng cách \({O_1},{\rm{ }}{O_2}\) lần lượt \(32\left( {cm} \right)\) và \(38\left( {cm} \right)\). Li độ của \(M\) sau thời điểm t một khoảng \(\dfrac{{31}}{{120}}s\) là:
Trả lời bởi giáo viên
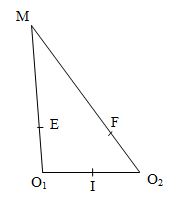
Ta có: ${u_1} = {u_2} = 6cos(40\pi t - \dfrac{\pi }{2}){\text{ }}\left( {mm} \right)$
+ Bước sóng $\lambda = \dfrac{v}{f} = \dfrac{{80}}{{20}} = 4(cm)$
+ Tại thời điểm t, sóng do nguồn ${O_1}$ vừa truyền tới trung điểm $I$ của đoạn ${O_1}{O_2}$
→ Sóng ở hai nguồn truyền đi được quãng đường $12{\rm{ }}cm = 3\lambda $ (hết thời gian $3T$)
Xét thời điểm sau thời điểm t một khoảng $\dfrac{{31}}{{120}}s = 5T + \dfrac{T}{6}$
Khi đó chỉ có sóng ở nguồn $1$ truyền đến $M$
Thật vậy, $EM{\rm{ }} = {\rm{ }}20cm{\rm{ }} = {\rm{ }}5\lambda $ → Cần thời gian $5T$ để sóng truyền từ $E$ đến $M$
→ sau $\dfrac{{31}}{{120}}s = 5T + \dfrac{T}{6}$ sóng nguồn $1$ truyền được đến $M$
$FM{\rm{ }} = {\rm{ }}26cm{\rm{ }} = {\rm{ }}6,5\lambda $ → Cần thời gian $6,5T$ để sóng truyền từ $F$ đến $M$
→ sau $\dfrac{{31}}{{120}}s = 5T + \dfrac{T}{6}$ sóng từ nguồn $2$ chưa đến $M$
Như vậy li độ của điểm M tại thời điểm sau thời điểm t một khoảng $\dfrac{{31}}{{120}}s = 5T + \dfrac{T}{6}$ là:
\(\begin{array}{l}{u_M} = {u_{1M}} = 6\cos (40\pi t - \dfrac{\pi }{2} - \dfrac{{2\pi {d_1}}}{\lambda })\\ = 6\cos \left[ {40\pi (3T + \dfrac{{31}}{{120}}) - \dfrac{\pi }{2} - \dfrac{{2\pi .32}}{4}} \right] = 3\sqrt 3 (cm)\end{array}\)
Hướng dẫn giải:
+ Sử dụng biểu thức tính bước sóng: \(\lambda = \dfrac{v}{f}\)
+ Sử dụng lí thuyết về truyền sóng

