Tại mặt chất lỏng có hai nguồn phát sóng kết hợp \(A,{\rm{ }}B\) cách nhau \(16{\rm{ }}cm\), dao động điều hòa theo phương vuông góc mặt chất lỏng với phương trình: \({u_A} = 2\cos 40\pi t\left( {cm} \right)\) và \({u_B} = 2\cos \left( {40\pi t + \pi } \right)\left( {cm} \right)\). Tốc độ truyền sóng trên mặt chất lỏng là \(40{\rm{ }}cm/s\). \(M\) là một điểm trên đường thẳng \(Ax\) vuông góc với \(AB\) mà tại đó các phần tử chất lỏng dao động với biên độ cực đại. Khoảng cách \(AM\) ngắn nhất bằng:
Trả lời bởi giáo viên
\(\lambda = \dfrac{v}{f} = \dfrac{{40}}{{20}} = 2cm\)
- Cách 1:
+ Số điểm dao động với biên độ cực đại trên đoạn AB:
\(\dfrac{{ - AB}}{\lambda } - \dfrac{1}{2} < k < \dfrac{{AB}}{\lambda } - \dfrac{1}{2}\)
\( \Rightarrow - 8,5 < k < 7,5\)
\( \to \) Có \(16\) điểm dao động với biên độ cực đại.
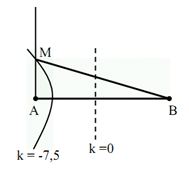
+ Điểm M gần A nhất thì M nhất định nằm trên vân cực đại ứng với bậc \(k = - 7,5\) (Số bán nguyên nhỏ hơn \(8,5\)).
\(MA - \sqrt {A{B^2} + M{A^2}} = - 7,5\lambda \)
\(MA - \sqrt {{{16}^2} + M{A^2}} = - 7,5.2 \Rightarrow MA = 1,03cm\)
- Cách 2:
+ Số dao động cực đại trên đoạn AB: \( - \dfrac{1}{2} - \dfrac{{AB}}{\lambda } \le k \le \dfrac{{AB}}{\lambda } - \dfrac{1}{2} \Leftrightarrow - 8,5 \le k \le 7,5\)
+ Để \(AM\) ngắn nhất thì \(M\) phải nằm trên hypebol cực đại \(k = - 8\)
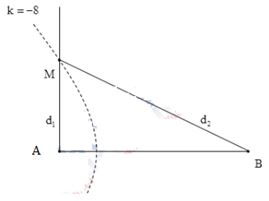
Từ hình vẽ ta có \(\left\{ \begin{array}{l}{d_2} - {d_1} = 15\\d_2^2 = 16 + d_1^2\end{array} \right. = > {\left( {{d_1} + 15} \right)^2} = {16^2} + d_1^2\)
Giải phương trình thu được \({d_1} = {\rm{ }}1,03{\rm{ }}cm\)
Hướng dẫn giải:
+ Sử dụng biểu thức tính bước sóng: \(\lambda = \dfrac{v}{f}\)
+ Sử dụng công thức tính số điểm dao động với biên độ cực đại trên đoạn thẳng nối hai nguồn trong giao thoa sóng hai nguồn ngược pha: \(\dfrac{{ - AB}}{\lambda } - \dfrac{1}{2} < k < \dfrac{{AB}}{\lambda } - \dfrac{1}{2}\)
+ Điều kiện có cực đại giao thoa của hai nguồn ngược pha: \({d_2}-{\rm{ }}{d_1} = \left( {k{\rm{ }} + {\rm{ }}\dfrac{1}{2}} \right)\lambda \)

