Câu hỏi:
2 năm trước
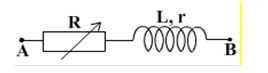
Cho mạch điện như hình. Biết điện áp \({u_{AB}} = 160\cos 100\pi t\left( V \right)\), \(r{\rm{ }} = {\rm{ }}15\Omega ,\) \(L = \dfrac{1}{{5\pi }}H\). Điều chỉnh biến trở \(R\) để công suất tiêu thụ trên \(R\) cực đại. Tính giá trị của \(R\) và \({P_{Rmax}}\).
Trả lời bởi giáo viên
Đáp án đúng: d
+ Hiệu điện thế hiệu dụng: \(U = \dfrac{{160}}{{\sqrt 2 }} = 80\sqrt 2 V\)
+ Cảm kháng: \({Z_L} = \omega L = 100\pi .\dfrac{1}{{5\pi }} = 20\Omega \)
+ Công suất tiêu thụ trên R max khi:
\(\begin{array}{l}{R^2} = {r^2} + {\left( {{Z_L} - {Z_C}} \right)^2}\\ \to R = \sqrt {{r^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} = \sqrt {{{15}^2} + {{\left( {20} \right)}^2}} = 25\Omega \end{array}\)
Công suất cực đại khi đó:
\({P_{{\rm{max}}}} = \dfrac{{{U^2}}}{{2{\rm{r}} + 2\sqrt {{r^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }} = \dfrac{{{{(80\sqrt 2 )}^2}}}{{2.15 + 2\sqrt {{{15}^2} + {{\left( {20} \right)}^2}} }} = 160{\rm{W}}\)
Hướng dẫn giải:
Bài toán mạch RLC mắc nối tiếp trong đó cuộn cảm không thuần cảm (có điện trở trong \(r \ne 0\))
Câu hỏi khác
- Bài tập mạch RLC mắc nối tiếp có lời giải MÔN LÝ lớp 12
- Bài tập các mạch điện xoay chiều có lời giải MÔN LÝ lớp 12
- Bài tập pha u,i - viết phương trình u, i có lời giải MÔN LÝ lớp 12
- Bài tập lý thuyết đại cương về dòng điện xoay chiều có lời giải MÔN LÝ lớp 12
- Bài tập đại cương dòng điện xoay chiều có lời giải MÔN LÝ lớp 12
