Câu hỏi:
2 năm trước
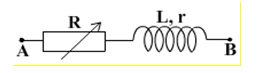
Cho mạch điện như hình. Biết điện áp \({u_{AB}} = 160\cos 100\pi t\left( V \right)\), \(r{\rm{ }} = {\rm{ }}15\Omega ,\) \(L = \dfrac{1}{{5\pi }}H\). Điều chỉnh biến trở R cho công suất tiêu thụ trên mạch cực đại. Tính \({P_{max}}\).
Trả lời bởi giáo viên
Đáp án đúng: a
+ Hiệu điện thế hiệu dụng: \(U = \dfrac{{160}}{{\sqrt 2 }} = 80\sqrt 2 V\)
+ Cảm kháng: \({Z_L} = \omega L = 100\pi .\dfrac{1}{{5\pi }} = 20\Omega \)
+ Công suất tiêu thụ trên mạch \({P_{max}}\) khi \(R + r = \left| {{Z_L} - {Z_C}} \right| = {Z_L} = 20\Omega \)
Khi đó, \({P_{max}} = \dfrac{{{U^2}}}{{2\left( {R + r} \right)}} = \dfrac{{{{\left( {80\sqrt 2 } \right)}^2}}}{{2.20}} = 320W\)
Hướng dẫn giải:
+ Sử dụng biểu thức tính cảm kháng: \({Z_L} = \omega L\)
+ Mạch có RLC, cuộn cảm có điện trở trong, khi đó công suất tiêu thụ trên mạch \({P_{max}}\) khi \(R + r = \left| {{Z_L} - {Z_C}} \right|\)
+ Vận dụng biểu thức tính công suất: \(P = \dfrac{{{U^2}}}{{{Z^2}}}R\)
Câu hỏi khác
- Bài tập mạch RLC mắc nối tiếp có lời giải MÔN LÝ lớp 12
- Bài tập các mạch điện xoay chiều có lời giải MÔN LÝ lớp 12
- Bài tập pha u,i - viết phương trình u, i có lời giải MÔN LÝ lớp 12
- Bài tập lý thuyết đại cương về dòng điện xoay chiều có lời giải MÔN LÝ lớp 12
- Bài tập đại cương dòng điện xoay chiều có lời giải MÔN LÝ lớp 12
