Hai nguồn phát sóng kết hợp S1, S2 trên mặt nước cách nhau 30 cm phát ra hai dao động điều hoà cùng phương, cùng tần số f = 50 Hz và pha ban đầu bằng không. Biết tốc độ truyền sóng trên mặt chất lỏng v = 6m/s. Những điểm nằm trên đường trung trực của đoạn S1S2 mà sóng tổng hợp tại đó luôn dao động ngược pha với sóng tổng hợp tại O ( O là trung điểm của S1S2) cách O một khoảng nhỏ nhất là:
Trả lời bởi giáo viên
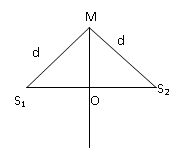
Giả sử hai sóng tại S1, S2 có dạng :
\({u_1} = {\rm{ }}{u_2} = {\rm{ }}acos\omega t\)
Gọi M là 1 điểm thỏa mãn bài toán (có 2 điểm thỏa mãn nằm đối xứng nhau qua S1,S2)
Phương trình dao động tại M:
\({u_M} = 2acos(\omega t - \frac{{2\pi d}}{\lambda })\) (d: Khoảng cách từ M đến S1, S2)
Phương trình dao động tại O:
\({u_O} = 2acos(\omega t - \frac{{2\pi {\rm{O}}{{\rm{S}}_1}}}{\lambda })\)
Theo bài ra:
\(\begin{array}{l}\Delta {\varphi _{M/O}} = {\varphi _M} - {\varphi _O} = \frac{{2\pi }}{\lambda }({\rm{O}}{{\rm{S}}_1} - d) = (2k + 1)\pi \to {\rm{O}}{{\rm{S}}_1} - d = \frac{\lambda }{2}(2k + 1)\\ \to d = {\rm{O}}{{\rm{S}}_1} - \frac{\lambda }{2}(2k + 1){\rm{ (*)}}\end{array}\)
Tam giác S1OM vuông nên:
$\begin{gathered}d{\text{ }} > {\text{ }}O{S_1} \to {\text{O}}{{\text{S}}_1} - \frac{\lambda }{2}(2k + 1) > {\text{ }}O{S_1} \hfill \\\leftrightarrow 2k + 1 < 0 \to k < - \frac{1}{2}(k \in Z) \hfill \\\end{gathered} $
Nhìn vào biểu thức (*) ta thấy dmin khi kmax = -1. (do OS1 không đổi nên dmin thì OM min )
Thay OS1 = S1S2/2 = 15cm;
\(\lambda = v/f = 600cm/50 = 12cm\)
k = -1 vào (*) ta được: d = 21cm
\(OM = \sqrt {{d^2} - {\rm{O}}{{\rm{S}}_1}^2} = \sqrt {{{21}^2} - {{15}^2}_{^{}}} = 216 = 6\sqrt 6 cm\)
Hướng dẫn giải:
+ Viết phương trình dao động
+ Áp dụng điều kiện dao động ngược pha:
\(\Delta \varphi = (2k + 1)\pi \)

