Ở mặt chất lỏng có hai nguồn sóng A, B cách nhau 18cm, dao động theo phương thẳng đứng với phương trình là \({u_A} = {u_B} = A.\cos 50\pi t\) (với t tính bằng s). Tốc độ truyền sóng ở mặt chất lỏng là 50cm/s. Gọi O là trung điểm của AB, điểm M ở mặt chất lỏng nằm trên đường trung trực của AB và gần O nhất sao cho phần tử chất lỏng tại M dao động cùng pha với phần tử chất lỏng tại O. Khoảng cách MO là
Trả lời bởi giáo viên
Ta có: \(\left\{ \begin{array}{l}f = 25Hz\\v = 50cm/s\end{array} \right. \Rightarrow \lambda = \dfrac{v}{f} = 2cm\)
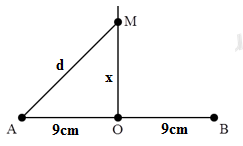
Phương trình dao động tại O:
\({u_O} = 2A.\cos \left( {50\pi t - \dfrac{{2\pi .OA}}{\lambda }} \right) = 2A.\cos \left( {50\pi t - \dfrac{{2\pi .9}}{2}} \right) = 2A.\cos \left( {50\pi t - 9\pi } \right)\)
Phương trình dao động tại M:
\({u_M} = 2A.\cos \left( {50\pi t - \dfrac{{2\pi .OM}}{\lambda }} \right) = 2A.\cos \left( {50\pi t - \dfrac{{2\pi .d}}{2}} \right) = 2A.\cos \left( {50\pi t - \pi d} \right)\)
M dao động cùng pha với O nên:
\(\begin{array}{l}\Delta \varphi = \pi d - 9\pi = k2\pi \Rightarrow d = 9 + 2k\\d > 9cm \Leftrightarrow 9 + 2k > 9 \Rightarrow k > 0 \Rightarrow k = 1;2;3;...\\{d_{\min }} \Leftrightarrow k = 1 \Rightarrow d = 9 + 2 = 11cm\end{array}\)
Áp dụng định lí Pitago ta có: \({x_{\min }} = \sqrt {d_{\min }^2 - {9^2}} = \sqrt {{{11}^2} - {9^2}} = \sqrt {40} = 2\sqrt {10} cm\)
Hướng dẫn giải:
+ Phương trình dao động của phần tử M nằm trên đường trung trực của AB có dạng:
\({u_M} = 2A.\cos \left( {\omega t - \dfrac{{2\pi d}}{\lambda }} \right)\)
Trong đó d là khoảng cách từ điểm M đến hai nguồn.
+ Hai dao động cùng pha khi: \(\Delta \varphi = 2k\pi \)

