Ở mặt chất lỏng có hai nguồn sóng A, B cách nhau 19 cm, dao động theo phương thẳng đứng với phương trình là \({u_A} = {\rm{ }}{u_B} = {\rm{ }}acos20\pi t\) (với t tính bằng s). Tốc độ truyền sóng của mặt chất lỏng là 40 cm/s. Gọi M là điểm ở mặt chất lỏng gần A nhất sao cho phần tử chất lỏng tại M dao động với biên độ cực đại và cùng pha với nguồn A. Khoảng cách AM là:
Trả lời bởi giáo viên
\(\lambda = \frac{v}{f} = 4cm\)
Cách 1:
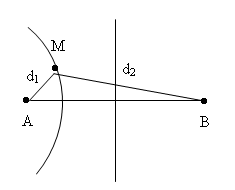
Xét điểm M: AM = d1; BM = d2
\(\begin{array}{l}{u_M} = acos(20\pi t{\rm{ }} - \frac{{2\pi {d_1}}}{\lambda }) + {\rm{ }}acos(20\pi t - \frac{{2\pi {d_2}}}{\lambda })\\ = 2acos(\frac{{\pi ({d_2} - {d_1})}}{\lambda })cos(20\pi t - \frac{{\pi ({d_1} + {d_2})}}{\lambda })\end{array}\)
Điểm M dao động với biên độ cực đại, cùng pha với nguồn A khi:
\(cos(\frac{{\pi ({d_2} - {d_1})}}{\lambda }) = 1\) và \(\frac{{\pi ({d_1} + {d_2})}}{\lambda } = 2k\pi \)
\( \to \left\{ \begin{array}{l}{d_2} - {d_1} = 2k'\lambda \\{d_2} + {d_1} = 2k\lambda \end{array} \right. \to {d_1} = \left| {k - k'} \right|\lambda \)
Điểm M gần A nhất ứng với \(k - k' = 1 \to {d_{1\min }} = \lambda = 4cm\)
Cách 2:
Số cực đại giao thoa:
\( - \frac{{AB}}{\lambda } \le k \le \frac{{AB}}{\lambda } \to k = - 4;\, - 3;......3;\,4.\)
Điểm M gần A nhất dao động với Amax ứng với k = 4 (hoặc -4).
Phương trình dao động tại điểm M là:
\({u_M} = 2a\cos (\omega t - \frac{{\pi ({d_1} + {d_2})}}{\lambda })\) .
Độ lệch pha dao động giữa nguồn A và M là:
\(\Delta \varphi = \frac{{\pi ({d_1} + {d_2})}}{\lambda }\)
Do M dao động cùng pha với nguồn A nên:
\(\Delta \varphi = \frac{{\pi ({d_1} + {d_2})}}{\lambda } = n.2\pi \to ({d_1} + {d_2}) = 2n\lambda = 8n\,(cm)\)(1)
Mặt khác:
\({d_1} + {d_2} \ge AB = 19\,cm\) (2).
Từ (1) và (2) ta có: \(n \ge 2,375\) Vậy n nhận các giá trị: 3, 4, 5……
Mặt khác: M dao động với biên độ cực đại nên:
\({d_2} - {d_1} = 4\lambda = 16\,(cm)\) (3)
Từ (1), (2) và (3) ta được:
\({d_1} = 4n - 8 \to {d_{1\min }} = 4.3 - 8 = 4\,(cm).\)
Hướng dẫn giải:
+ Áp dụng biểu thức xác định bước sóng:
\(\lambda = \frac{v}{f}\)
+ Viết phương trình dao động sóng
+ Áp dụng điều kiện dao động cùng pha:
\(\Delta \varphi = k2\pi \)

