Trong thí nghiệm giao thoa sóng mặt nước, 2 nguồn sóng S1 và S2 cách nhau 11cm và dao động điều hòa theo phương vuông góc với mặt nước có cùng phương trình \({u_1} = {u_2} = 5c{\rm{os}}\left( {50\pi t} \right)mm\) . Tốc độ truyền sóng v = 0,5 m/s và biên độ sóng không đổi khi truyền đi. Chọn hệ trục xOy thuộc mặt phẳng mặt nước khi yên lặng, gốc O trùng với S1, Ox trùng S1S2. Trong không gian, phía trên mặt nước có 1 chất điểm chuyển động mà hình chiếu (P) của nó với mặt nước chuyển động với phương trình y = 12 - x và có tốc độ \({v_1} = 5\sqrt 2 cm/s\). Trong thời gian t = 2 (s) kể từ lúc (P) có tọa độ x = 0 thì (P) cắt bao nhiêu vân cực tiểu trong vùng giao thoa của sóng?
Trả lời bởi giáo viên
Ta có:
\(\lambda = \dfrac{v}{f} = \dfrac{v}{{\dfrac{\omega }{{2\pi }}}} = \dfrac{{0,5}}{{\dfrac{{50}}{{2\pi }}}} = 0,02m = 2cm\)
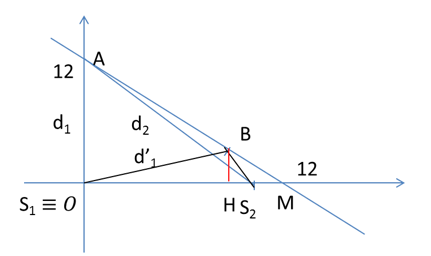
Trong không gian có một chất điểm dao động mà hình chiếu của nó lên mặt nước là đường thẳng \(y = 12 - x\).
Vận tốc chuyển động là: \({v_1} = 5\sqrt 2 cm/s\)
Sau \(2s\), quãng đường mà vật đi được là: \(S = AB = {v_1}t = 10\sqrt 2 cm\)
Tại B cách S1, S2 những khoảng d’1, d’2.
Gọi H - hình chiếu của B trên S1S2
S2M = 1cm
HM = 2cm = HB
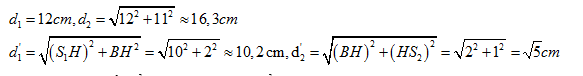
Trên đoạn BM số điểm có biên độ cực tiểu thỏa mãn:
\(\begin{array}{l}d{'_2} - d{'_1} \le (k + \dfrac{1}{2})\lambda \le {d_2} - {d_1}\\ \leftrightarrow - 4,48 \le k \le 1,65\\ \to k = - 4, - 3, - 2, - 1,0,1\end{array}\).
=> Có 6 điểm
Hướng dẫn giải:
+ Áp dụng biểu thức xác định bước sóng: \(\lambda = \dfrac{v}{f}\)
+ Áp dụng điều kiện biên độ cực tiểu của 2 nguồn cùng pha:
\({d_2} - {d_1} = (2k + 1)\dfrac{\lambda }{2}\)

