Trong thí nghiệm giao thoa sóng trên mặt nước, hai nguồn S1, S2 cách nhau 20cm dao động theo phương thẳng đứng với các phương trình u1 = u2 = Acos(ωt). Bước sóng trên mặt nước do hai nguồn này tạo ra là 4cm. Trên mặt nước, xét một vân giao thoa cực đại gần đường trung trực của S1S2 nhất. Số điểm dao động cùng pha với S1, S2 nằm trên vân này và thuộc hình tròn đường kính S1S2 là
Trả lời bởi giáo viên
Xét tại điểm M và N đều nằm trên cực đại giao thoa gần trung trực nhất với M nằm trên đường kính S1S2 và N nằm trên đường tròn đường kính S1S2
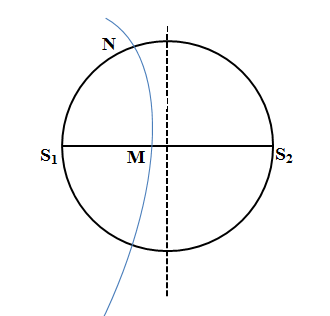
MS2 – MS1 = λ = 4cm
MS2 + MS1 = S1S2 = 20cm
=> MS2 = 12cm, MS1 = 8cm
NS2 – NS1 = 4cm
ΔNS1S2 vuông tại N nên \(NS_{2}^{2}+NS_{1}^{2}={{S}_{1}}{{S}_{2}}^{2}={{20}^{2}}\)
=> NS1 = 12cm, NS2= 16cm
Xét trên đoạn MN, số điểm dao động cùng pha với nguồn phải thỏa mãn:
\(\frac{\pi ({{d}_{1}}+{{d}_{2}})}{\lambda }=2k\pi \Rightarrow M{{S}_{1}}+M{{S}_{2}}\le {{d}_{1}}+{{d}_{2}}=2k\lambda \le N{{S}_{1}}+N{{S}_{2}}\)
=> 20 ≤ 8k ≤ 28 => 2,5≤ k ≤ 3,5 => có 1 giá trị k nguyên ứng với 1 điểm cùng pha với hai nguồn
Vậy trên hai nửa hypebol có 2 điểm dao động cùng pha với hai nguồn.
Hướng dẫn giải:
Tại M nằm trên cực đại bậc k khi khoảng cách từ M tới hai nguồn thỏa mãn d2 – d1 = kλ
Nếu hai nguồn cùng pha thì độ lệch pha của sóng tổng hợp tại điểm cách hai nguồn đoạn d1,d2 so với hai nguồn bằng \(\Delta \varphi =\frac{\pi ({{d}_{1}}+{{d}_{2}})}{\lambda }\)
Hai điểm dao động cùng pha thì Δφ = 2kπ

