Trên mặt nước có hai nguồn sóng giống nhau A và B, cách nhau khoảng AB = 12(cm) đang dao động vuông góc với mặt nước tạo ra sóng có bước sóng \(\lambda = {\rm{ }}1,6cm\) . C và D là hai điểm khác nhau trên mặt nước, cách đều hai nguồn và cách trung điểm O của AB một khoảng 8(cm). Số điểm dao động cùng pha với nguồn ở trên đoạn CD là
Trả lời bởi giáo viên
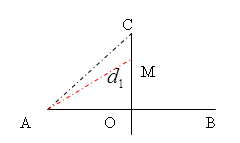
Cách 1:
Tính trên CD:
\(AO \leqslant {d_2} - {\text{ }}{d_1} = k\lambda \leqslant AC\)
$ \Leftrightarrow \frac{6}{{1,6}} < k < \frac{{1,0}}{{1,6}} \Leftrightarrow k = 4,5,6$
Þ Có tất cả 6 giá trị k thoả mãn
Cách 2: Phương trình tổng hợp tại 1 điểm trên OD:
\(u = 2a\cos (2\pi ft - \pi \frac{{2d}}{\lambda })\)
Cùng pha=>
\(\pi \frac{{2d}}{\lambda } = 2k\pi \Rightarrow d = 1,6\lambda \) có \(6 \le d = 1,6k \le 10 \Rightarrow k = 4;5;6\) do tính đối xứng nên có 6 điểm
Hướng dẫn giải:
Áp dụng điều kiện dao động cùng pha: \(\Delta \varphi = k2\pi \)

