Trên mặt nước có hai nguồn kết hợp AB cùng pha cách nhau một đoạn 12cm đang dao động vuông góc với mặt nước tạo ra sóng với bước sóng 1,6cm. Gọi C là một điểm trên mặt nước cách đều hai nguồn và cách trung điểm O của đoạn AB một khoản 8cm. Hỏi trên đoạn CO, số điểm dao động cùng pha với nguồn là:
Trả lời bởi giáo viên
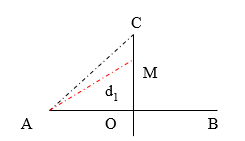
+ Do hai nguồn dao động cùng pha nên để đơn giản ta cho pha ban đầu của chúng bằng 0.
+ Độ lệch pha giữa hai điểm trên phương truyền sóng:
\(\Delta \varphi = \dfrac{{2\pi d}}{\lambda }\).
+ Xét điểm M trên đường trung trực của AB cách A một đoạn d1 và cách B một đoạn d2. Suy ra d1=d2.
+ Mặt khác điểm M dao động cùng pha với nguồn nên
\(\Delta \varphi = \dfrac{{2\pi {d_1}}}{\lambda } = k2\pi \to {d_1} = k\lambda = 1,6k(1)\).
+ Mà :
\(AO \le {d_1} \le AC \to \dfrac{{AB}}{2} \le 1,6k \le \sqrt {{{\left( {\dfrac{{AB}}{2}} \right)}^2} + O{C^2}} \)
(Do \(AO = \dfrac{{AB}}{2}\) và \(AC = \sqrt {{{\left( {\dfrac{{AB}}{2}} \right)}^2} + O{C^2}} = 10(cm)\))
\(\Rightarrow \)\(6 \le 1,6k \le 10 \Rightarrow 3,75 \le k \le 6,25 \Rightarrow k = 4;5;6\)
=> Trên đoạn CO có 3 điểm dao dộng cùng pha với nguồn.
Hướng dẫn giải:
+ Áp dụng biểu thức độ lệch pha giữa hai điểm:
\(\Delta \varphi = \dfrac{{2\pi d}}{\lambda }\)
+ Áp dụng điều kiện dao động cùng pha :
\(\Delta \varphi = k2\pi \)

