Ba điểm A, B, C trên mặt nước là 3 đỉnh của tam giác đều có cạnh bằng 8cm, trong đó A và B là 2 nguồn phát sóng giống nhau, có bước sóng 0,8cm. Điểm M trên đường trung trực của AB, dao động cùng pha với điểm C và gần C nhất thì phải cách C một khoảng bao nhiêu?
Trả lời bởi giáo viên
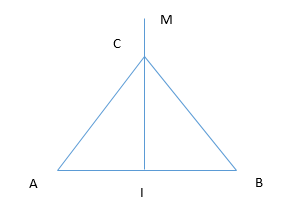
Ta có hai điểm \(M\) và \(C\) cùng pha:
\(\dfrac{{2\pi AC}}{\lambda } - \dfrac{{2\pi AM}}{\lambda } = 2k\pi \)
Suy ra:
\(AC{\rm{ }}-{\rm{ }}AM{\rm{ }} = \lambda \)
Xét điểm \(M\) nằm trong khoảng \(CO\) (\(O\) là trung điểm \(AB\)). Suy ra \(AM = AC - \lambda = 8 - 0,8\)
\(CM{\rm{ }} = {\rm{ }}CO{\rm{ }}-{\rm{ }}MO{\rm{ }} = \sqrt {A{C^2} - A{O^2}} - \sqrt {A{M^2} - A{O^2}} \) (với \(AC = 8 cm, AO = 4cm\))
Suy ra \(CM = 0,94 cm\) (loại)
Xét điểm M nằm ngoài đoạn \(CO\).
Suy ra:
\(AM{\rm{ }} = {\rm{ }}AC{\rm{ }} + \lambda = {\rm{ }}8{\rm{ }} + {\rm{ }}0,8\)
\(CM{\rm{ }} = {\rm{ }}MO{\rm{ }}-{\rm{ }}CO{\rm{ }} = \sqrt {A{M^2} - A{O^2}} - \sqrt {A{C^2} - A{O^2}} \) (với \(AC = 8 cm, AO = 4cm\)).
Suy ra \(CM = 0,91cm\) (nhận)
Vậy khoảng cách ngắn nhất giữa \(M\) và \(C\) dao động cùng pha là \(0,91 cm\).
Hướng dẫn giải:
Áp dụng điều kiện dao động cùng pha:
\(\Delta \varphi = k2\pi \)

