Hai mũi nhọn A, B cách nhau \(8 cm\) gắn vào đầu một cần rung có tần số \(f = 100 Hz\), đặt chạm nhẹ vào mặt một chất lỏng. Tốc độ truyền sóng trên mặt chất lỏng \(v = 0,8 m/s\). Hai nguồn A, B dao động theo phương thẳng đứng với cùng phương trình \({u_A} = {\rm{ }}{u_B} = {\rm{ }}acos(\omega t){\rm{ }}cm.\) Một điểm M trên mặt chất lỏng cách đều A, B một khoảng \(d = 8 cm\). Tìm trên đường trung trực của AB hai điểm M1,M2 gần M nhất và dao động cùng pha với M.
Trả lời bởi giáo viên
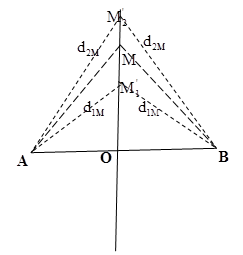
Ta có:
+ Bước sóng: \(\lambda = \dfrac{v}{f} = \dfrac{{0,8}}{{100}} = {8.10^{ - 3}}m = 0,8cm\)
+ Ta có phương trình giao thoa sóng trên đường trung trực của S1S2 là:
\(u = 2Ac{\rm{os}}\left( {\dfrac{\pi }{\lambda }\left( {{d_1} - {d_2}} \right)} \right){\rm{cos}}\left( {\omega t - \dfrac{\pi }{\lambda }\left( {{d_1} + {d_2}} \right)} \right)\)
theo giả thuyết hai sóng cùng pha trên đường trung trực nên ta có:
\(\left( {\dfrac{\pi }{\lambda }\left( {{d_{1M}} + {d_{2M}}} \right) - \dfrac{\pi }{\lambda }\left( {{d_{1{M_1}}} + {d_{2{M_1}}}} \right)} \right) = 2k\pi {\rm{ (1}})\)
mà
\({d_{1M}} = {\rm{ }}{d_{2M}} = {\rm{ }}{d_M} = {\rm{ }}8{\rm{ }}cm\)
\({d_{1M1}} = {\rm{ }}{d_{2M1}} = {\rm{ }}{d_{M1}}\)
từ (1) suy ra
\({d_M}-{\rm{ }}{d_{M1}} = {\rm{ }}\lambda {\rm{ }}\left( {{\rm{ }}\lambda = {\rm{ }}0,8/100{\rm{ }} = {\rm{ }}0,8{\rm{ }}cm} \right)\)
\({d_{M1}} = {\rm{ }}{d_M}-{\rm{ }}\lambda {\rm{ }} = {\rm{ }}8{\rm{ }}-{\rm{ }}0,8{\rm{ }} = {\rm{ }}7,2{\rm{ }}\left( {cm} \right)\)
suy ra:
\(O{M_1} = \sqrt {d_{{M_1}}^2 - O{A^2}} = \sqrt {7,{2^2} - {4^2}} = 5,99cm\)
\({d_{M2}} = {\rm{ }}{d_M} + {\rm{ }}\lambda {\rm{ }} = {\rm{ }}8{\rm{ }} + {\rm{ }}0,8{\rm{ }} = {\rm{ }}8,8{\rm{ }}\left( {cm} \right)\)
suy ra:
\(O{M_2} = \sqrt {d_{{M_2}}^2 - O{A^2}} = \sqrt {8,{8^2} - {4^2}} = 7,84cm\)
mà
\(OM = \sqrt {d_1^2 - O{A^2}} = \sqrt {{8^2} - {4^2}} = 6,93cm\)
vậy:
\(M{M_1} = OM - O{M_1} = 0,94cm \to {M_2}M = O{M_2} - OM = 0,91cm\)
Hướng dẫn giải:
+ Áp dụng biểu thức tính bước sóng: \(\lambda = \dfrac{v}{f}\)
+ Viết phương trình tổng hợp dao động sóng
+ Áp dụng điều kiện dao động cùng pha: \(\Delta \varphi = 2k\pi \)

