Cho hình chóp $S.ABC$ có tam giác $ABC$ vuông cân tại $B$, $AB = BC = a$, $SA = a\sqrt 3 $, $SA \bot \left( {ABC} \right)$. Góc giữa hai mặt phẳng $\left( {SBC} \right)$ và $\left( {ABC} \right)$ là
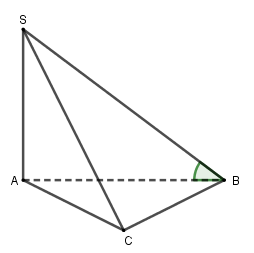
Ta có $BC \bot \left( {SAB} \right)$$ \Rightarrow BC \bot SA$. Góc giữa hai mặt phẳng $\left( {SBC} \right)$ và $\left( {ABC} \right)$ là góc $\widehat {SBA}$. $\tan \widehat {SBA} = \dfrac{{SA}}{{AB}}$$ = \dfrac{{a\sqrt 3 }}{a}$$ = \sqrt 3 $$ \Rightarrow \widehat {SBA} = 60^\circ $.
Cho tứ diện \(S.ABC\) có các cạnh \(SA\), \(SB\); \(SC\) đôi một vuông góc và \(SA = SB = SC = 1\). Tính \(\cos \alpha \), trong đó \(\alpha \) là góc giữa hai mặt phẳng \(\left( {SBC} \right)\) và \(\left( {ABC} \right)\)?
Cách 1:
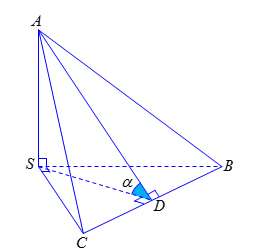
Gọi \(D\) là trung điểm cạnh \(BC\).
Ta có \(\left\{ \begin{array}{l}SA \bot SB\\SA \bot SC\end{array} \right. \Rightarrow SA \bot \left( {SBC} \right)\)\( \Rightarrow SA \bot BC\).
Mà \(SD \bot BC\) nên \(BC \bot \left( {SAD} \right)\).
\( \Rightarrow \left( {\widehat {\left( {SBC} \right),\left( {ABC} \right)}} \right) = \widehat {SDA} = \alpha \).
Khi đó tam giác \(SAD\) vuông tại \(S\) có \(SD = \dfrac{1}{{\sqrt 2 }}\); \(AD = \dfrac{{\sqrt 3 }}{{\sqrt 2 }}\) và \(\cos \alpha = \dfrac{{SD}}{{AD}}\) \( \Leftrightarrow \cos \alpha = \dfrac{1}{{\sqrt 3 }}\).
Cho hình chóp tứ giác đều có tất cả các cạnh đều bằng \(a\). Tính cosin của góc giữa một mặt bên và một mặt đáy.
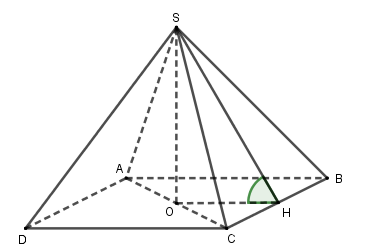
Gọi \(O\) là trung điểm của \(AC\). Vì $S.ABCD$ là hình chóp đều nên \(SO \bot \left( {ABCD} \right)\).
Gọi \(H\) là trung điểm của \(BC\) và góc giữa mặt bên \(\left( {SBC} \right)\) và mặt đáy \(\left( {ABCD} \right)\) là \(\alpha \).
Ta có \(\left( {SBC} \right) \cap \left( {ABCD} \right) = BC\) mà \(BC \bot SH\) và \(BC \bot OH\) nên \(\widehat {SHO} = \alpha \).
\(SH\) là đường cao của tam giác đều \(SBC\) cạnh \(a\) nên \(SH = \dfrac{{a\sqrt[{}]{3}}}{2}\),
Xét tam giác \(SOH\) vuông tại \(O\) có: \(\cos \alpha = \dfrac{{OH}}{{SH}}\)\( = \dfrac{{\dfrac{a}{2}}}{{\dfrac{{a\sqrt[{}]{3}}}{2}}} = \dfrac{1}{{\sqrt[{}]{3}}}\).
Giả sử $\alpha $ là góc của hai mặt của một tứ diện đều có cạnh bằng $a$. Khẳng định đúng là
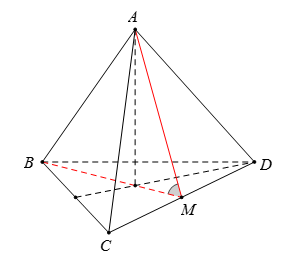
Gọi $M$ là trung điểm cạnh $CD$ của tứ diện đều $ABCD$.
Ta có $\left\{ \begin{array}{l}\left( {ACD} \right) \cap \left( {BCD} \right) = CD\\AM \subset \left( {ACD} \right):AM \bot CD\\BM \subset \left( {BCD} \right):BM \bot CD\end{array} \right.$ $ \Rightarrow $ $\left( {\widehat {\left( {ACD} \right),\left( {BCD} \right)}} \right) = \left( {\widehat {AM,BM}} \right) = \widehat {AMB} = \alpha $.
Tính: $AB = a$, $AM = BM = \dfrac{{a\sqrt 3 }}{2}$.
$cos\alpha = \cos \widehat {AMB} = \dfrac{{A{M^2} + B{M^2} - A{B^2}}}{{2.AM.BM}} = \dfrac{{2.{{\left( {\dfrac{{a\sqrt 3 }}{2}} \right)}^2} - {a^2}}}{{2.\dfrac{{a\sqrt 3 }}{2}.\dfrac{{a\sqrt 3 }}{2}}} = \dfrac{1}{3}$.
$ \Rightarrow {\tan ^2}\alpha = \dfrac{1}{{{{\cos }^2}\alpha }} - 1 = 8 \Rightarrow \tan \alpha = \sqrt 8 $.
Cho hình chóp tứ giác đều có cạnh đáy bằng \(a\) và chiều cao bằng $\dfrac{{a\sqrt 3 }}{2}$. Tính số đo của góc giữa mặt bên và mặt đáy.
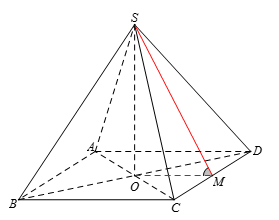
Gọi $O$ là tâm hình vuông $ABCD$, $M$ là trung điểm $CD$.
\(\left\{ \begin{array}{l}\left( {SCD} \right) \cap \left( {ABCD} \right) = CD\\SM \subset \left( {SCD} \right):{\rm{ }}SM \bot CD\\OM \subset \left( {ABCD} \right):{\rm{ }}OM \bot CD\end{array} \right.\) \( \Rightarrow \left( {\widehat {\left( {SCD} \right),\left( {ABCD} \right)}} \right) = \left( {\widehat {SM,OM}} \right) = \widehat {SMO}\).
$\tan \widehat {SMO} = \dfrac{{SO}}{{OM}} = \dfrac{{\dfrac{{a\sqrt 3 }}{2}}}{{\dfrac{a}{2}}} = \sqrt 3 $ $ \Rightarrow \widehat {SMO} = 60^\circ $.
Cho hình chóp \(S.ABCD\) đáy \(ABCD\) là hình chữ nhật, \(AB = a\), \(AD = 2a\). Cạnh bên \(SA\) vuông góc với đáy \(\left( {ABCD} \right)\), \(SA = 2a\). Tính \(\tan \) của góc giữa hai mặt phẳng \(\left( {SBD} \right)\) và \(\left( {ABCD} \right)\).
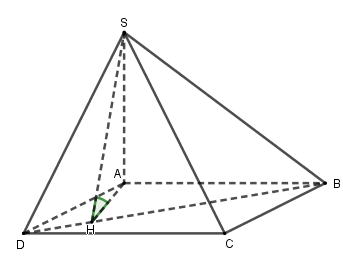
Kẻ \(AH \bot BD\), \(\left( {H \in BD} \right)\) (1).
\(\left\{ \begin{array}{l}BD \bot SA\,\,\,\left( {SA \bot \left( {ABCD} \right)} \right)\\BD \bot AH\end{array} \right.\) \( \Rightarrow BD \bot \left( {SAH} \right)\) \( \Rightarrow BD \bot SH\) (2).
Và: \(\left( {SBD} \right) \cap \left( {ABCD} \right) = BD\) (3).
Từ (1) (2) và (3) suy ra: Góc giữa hai mặt phẳng \(\left( {SBD} \right)\) và \(\left( {ABCD} \right)\)là \(\widehat {SHA}\).
Xét \(\Delta ABD\) vuông tại \(A\): \(\dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{D^2}}}\)\( = \dfrac{1}{{{a^2}}} + \dfrac{1}{{4{a^2}}}\)\( = \dfrac{5}{{4{a^2}}}\) $ \Rightarrow AH = \dfrac{{2a}}{{\sqrt 5 }}$.
Xét \(\Delta SAH\) vuông tại \(A\): \(\tan \widehat {SHA} = \dfrac{{SA}}{{AH}} = \sqrt 5 \).
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông tại đỉnh \(A\), cạnh \(BC = a\), \(AC = \dfrac{{a\sqrt 6 }}{3}\) các cạnh bên \(SA = SB = SC = \dfrac{{a\sqrt 3 }}{2}\). Tính góc tạo bởi mặt bên \(\left( {SAB} \right)\) và mặt phẳng đáy \(\left( {ABC} \right)\).
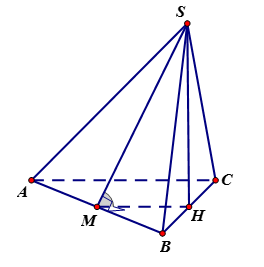
Vì \(SA = SB = SC = \dfrac{{a\sqrt 3 }}{2}\) nên hình chiếu của \(S\) trùng với \(H\) là tâm đường tròn ngoại tiếp đáy \(ABC\). Nhận xét \(H\) là trung điểm \(BC\).
Gọi \(M\) là trung điểm \(AB\), nhận xét \(AB \bot \left( {SMH} \right)\) nên góc tạo bởi mặt bên \(\left( {SAB} \right)\) và mặt phẳng đáy \(\left( {ABC} \right)\) là góc \(\widehat {SMH}\).
Xét tam giác \(SBH\) có \(SH = \sqrt {S{B^2} - B{H^2}} = \dfrac{{a\sqrt 2 }}{2}\).
Xét tam giác \(SMH\) có \(\tan \widehat M = \dfrac{{SH}}{{MH}} = \dfrac{{\dfrac{{a\sqrt 2 }}{2}}}{{\dfrac{{a\sqrt 6 }}{6}}} = \sqrt 3 \) \( \Leftrightarrow \widehat M = {60^{\rm{o}}}\).
Cho hình chóp \(S.ABC\) có cạnh \(SA\) vuông góc với mặt phẳng \(\left( {ABC} \right)\), biết \(AB = AC = a\), \(BC = a\sqrt 3 \). Tính góc giữa hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SAC} \right)\).
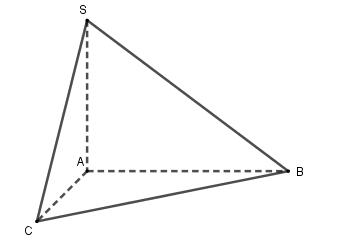
Vì \(SA \bot \left( {ABC} \right)\) nên \(SA \bot AB\) và \(SA \bot AC\).
ta có: $\left\{ \begin{array}{l}\left( {SAB} \right) \cap \left( {SAC} \right) = SA\\SA \bot AB\\SA \bot AC\end{array} \right.$ $ \Rightarrow \left( {\widehat {\left( {SAB} \right),\left( {SAC} \right)}} \right) = \left( {\widehat {AB,AC}} \right)$.
Xét $\Delta ABC$ có $\cos \widehat {BAC} = \dfrac{{A{B^2} + A{C^2} - B{C^2}}}{{2.AB.AC}}$ $ = \dfrac{{{a^2} + {a^2} - {{\left( {a\sqrt 3 } \right)}^2}}}{{2.a.a}} = - \dfrac{1}{2}$ $ \Rightarrow \widehat {BAC} = 120^\circ $.
Do đó $\left( {\widehat {AB,AC}} \right) = {180^0} - {120^0} = {60^0}$ (vì góc giữa hai đường thẳng không thể lớn hơn \({90^0}\)).
Vậy góc giữa hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SAC} \right)\) là \({60^0}\).
Cho hình chóp \(S.ABC\) có \(SA \bot (ABC),\,SA = 2a.\) Tam giác\(ABC\)vuông tại B \(\,AB = a\), \(BC = a\sqrt 3 \). Tính cosin của góc \(\varphi \) tạo bởi hai mặt phẳng \((SAC)\) và \((SBC).\)
Cách 1:
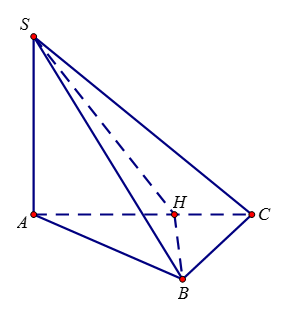
Kẻ \(BH \bot AC\,\,\,\,\, \Rightarrow BH \bot (SAC)\). Áp dụng công thức \(S' = S\cos \phi \) trong đó \(S' = dt\left( {SHC} \right)\),
\(S = dt\left( {SBC} \right)\), \(\phi \) là góc hợp bởi hai mặt phẳng \(\left( {SBC} \right)\) và \(\left( {SAC} \right)\)
Dễ thấy tam giác \(SBC\) vuông tại B và \(SB = a\sqrt 5 \). \(dt\left( {SBC} \right) = \dfrac{{{a^2}\sqrt {15} }}{2}\)
\(CH = \dfrac{{B{C^2}}}{{AC}} = \dfrac{3}{2}a\), \(dt\left( {SHC} \right) = \dfrac{3}{2}{a^2}\). Vậy \(\cos \phi = \dfrac{{\sqrt {15} }}{5}\)
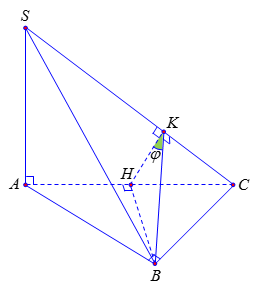
Cho hình chóp \(S.ABC\) có đáy là tam giác vuông cân tại \(B\), cạnh bên \(SA\) vuông góc với mặt phẳng đáy, \(AB = BC = a\) và \(SA = a\). Góc giữa hai mặt phẳng \(\left( {SAC} \right)\) và \(\left( {SBC} \right)\) bằng
Gọi \(H\) là trung điểm cạnh \(AC\)
Ta có \(\left( {SAC} \right) \bot \left( {ABC} \right)\) (vì \(SA \bot \left( {ABC} \right)\)) và \(BH \bot AC\)\( \Rightarrow BH \bot \left( {SAC} \right)\).
Trong mặt phẳng \(\left( {SAC} \right)\), kẻ \(HK \bot SC\) thì \(SC \bot \left( {BHK} \right)\)\( \Rightarrow SC \bot BK\).
\( \Rightarrow \left( {\widehat {\left( {SAC} \right),\,\left( {SBC} \right)}} \right) = \widehat {SKH} = \varphi \).
Mặt khác
Tam giác \(ABC\) vuông cân tại \(B\) có \(AB = BC = a\) nên \(AC = a\sqrt 2 \) và \(BH = \dfrac{{a\sqrt 2 }}{2}\).
Hai tam giác \(CKH\) và $CAS$ đồng dạng nên \(HK = \dfrac{{HC.SA}}{{SC}}\) \( \Leftrightarrow HK = \dfrac{{HC.SA}}{{\sqrt {S{A^2} + A{C^2}} }} = \dfrac{{a\sqrt 2 }}{{\sqrt 3 }}\).
Tam giác \(BHK\) vuông tại \(H\) có \(\tan \varphi = \dfrac{{BH}}{{BK}} = \sqrt 3 \) \( \Rightarrow \varphi = 60^\circ \).
Vậy \(\left( {\widehat {\left( {SAC} \right),\,\left( {SBC} \right)}} \right) = 60^\circ \).
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thoi tâm $O$, đường thẳng $SO$ vuông góc với mặt phẳng $\left( {ABCD} \right)$. Biết \(BC = SB = a,SO = \dfrac{{a\sqrt 6 }}{3}\). Tìm số đo của góc giữa hai mặt phẳng $\left( {SBC} \right)$và $\left( {SCD} \right)$.
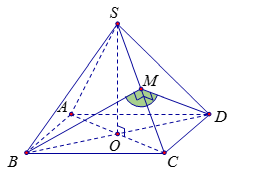
Gọi \(M\) là trung điểm của \(SC\), do tam giác \(SBC\) cân tại \(B\) nên ta có \(SC \bot BM\) (1).
Theo giả thiết ta có \(BD \bot \left( {SAC} \right) \Rightarrow SC \bot BD\). Do đó $SC \bot \left( {BCM} \right)$ suy ra $SC \bot DM$ (2).
Từ (1) và (2) suy ra góc giữa hai mặt phẳng \(\left( {SBC} \right)\) và \(\left( {SCD} \right)\) là góc giữa hai đường thẳng \(BM\) và $DM$.
Ta có \(\Delta SBO = \Delta CBO\) suy ra \(SO = CO = \dfrac{{a\sqrt 6 }}{3}\).
Do đó \(OM = \dfrac{1}{2}SC = \dfrac{{a\sqrt 3 }}{3}\).
Mặt khác \(OB = \sqrt {S{B^2} - S{O^2}} = \dfrac{{a\sqrt 3 }}{3}\). Do đó tam giác \(BMO\) vuông cân tại \(M\) hay góc \(\widehat {BMO} = 45^\circ \), suy ra \(\widehat {BMD} = 90^\circ \).
Vậy góc giữa hai mặt phẳng \(\left( {SBC} \right)\) và \(\left( {SCD} \right)\) là \(90^\circ \).
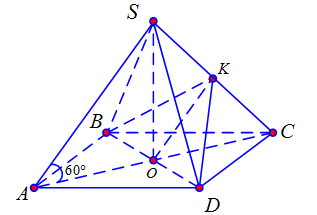
Cho hình chóp đều $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a\sqrt 2 $, biết các cạnh bên tạo với đáy một góc $60^\circ $. Giá trị lượng giác tang của góc giữa hai mặt phẳng $\left( {SAC} \right)$ và $\left( {SCD} \right)$ bằng
Kẻ $OK \bot SC$. Do $S.ABCD$ là hình chóp đều và $ABCD$ là hình vuông nên $SO \bot \left( {ABCD} \right)$; $BD \bot \left( {SAC} \right) \Rightarrow SC \bot BD$. Suy ra $SC \bot \left( {BKD} \right) \Rightarrow KD \bot SC$.
Vậy góc giữa hai mặt phẳng $\left( {SAC} \right)$ và $\left( {SCD} \right)$ là $\widehat {OKD}$ và $\tan \widehat {OKD} = \dfrac{{OD}}{{OK}}$ (do $\Delta KOD$ vuông ở $O$): $ABCD$ là hình vuông cạnh $a\sqrt 2 $ nên $AC = 2a \Rightarrow OA = OC = OD = a$.
Trong hình chóp đều $S.ABCD$, cạnh bên tạo với đáy một góc $60^\circ $ nên $\widehat {SAC} = 60^\circ $
$ \Rightarrow SO = OA.\tan 60^\circ = a\sqrt 3 $.
Ta có $\dfrac{1}{{O{K^2}}} = \dfrac{1}{{S{O^2}}} + \dfrac{1}{{O{C^2}}} \Rightarrow OK = \dfrac{{a\sqrt 3 }}{2}$$ \Rightarrow \tan \widehat {OKD} = \dfrac{{OD}}{{OK}} = \dfrac{2}{{\sqrt 3 }} = \dfrac{{2\sqrt 3 }}{3}$.
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang vuông tại \(A\) và \(D\), \(AB = 2a\), \(AD = DC = a\), \(SA = \,a\sqrt 2 \), \(SA \bot \left( {ABCD} \right)\). Tính cosin của góc giữa hai mặt phẳng \(\left( {SBC} \right)\) và \(\left( {SCD} \right)\).
Cách 1:
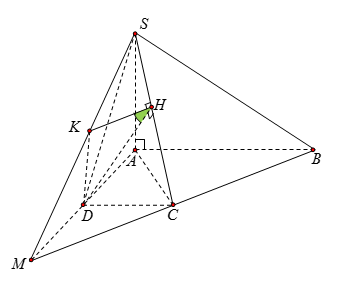
Gọi \(M = BC \cap AD\). Khi đó: \(\left( {\widehat {\left( {SBC} \right),\left( {SCD} \right)}} \right) = \left( {\widehat {\left( {SCM} \right),\left( {SCD} \right)}} \right)\)
Gọi \(H\) là hình chiếu của \(D\) lên \(SC\), kẻ \(HK\,{\rm{//}}\,MC\)\(\left( {K \in SM} \right)\) ta có:
\(\left( {\widehat {\left( {SCM} \right),\left( {SCD} \right)}} \right) = \widehat {KHD} = \alpha \)
Xét \(\Delta SCD\) vuông tại \(D\) ta có: \(\dfrac{1}{{D{H^2}}} = \dfrac{1}{{D{C^2}}} + \dfrac{1}{{D{S^2}}} = \dfrac{1}{{{a^2}}} + \dfrac{1}{{3{a^2}}} = \dfrac{4}{{3{a^2}}}\)\( \Rightarrow DH = \dfrac{{a\sqrt 3 }}{2}\).
\(HC = \dfrac{{D{C^2}}}{{SC}} = \dfrac{{{a^2}}}{{2a}} = \dfrac{a}{2}\).
Do \(HK\,{\rm{//}}\,MC\) mà \(\dfrac{{SH}}{{SC}} = \dfrac{3}{4}\) nên \(HK = \dfrac{3}{4}a\sqrt 2 = \dfrac{{3\sqrt 2 a}}{4}\); \(KM = \dfrac{1}{4}SM = \dfrac{{a\sqrt 6 }}{4}\).
Mặt khác ta có: \(\widehat {KDM} = \widehat {DSA}\) mà \(\sin \widehat {KMD} = \sin \widehat {DSA} = \dfrac{1}{{\sqrt 3 }}\) nên \(\widehat {KDM} = \widehat {KMD}\).
Do đó: \(KD = KM = \dfrac{{a\sqrt 6 }}{4}\).
Xét tam giác \(KDH\) ta có: \(\cos \alpha = \dfrac{{H{D^2} + H{K^2} - K{D^2}}}{{2HK.HD}} = \dfrac{{\sqrt 6 }}{3}\).
Cho hình lăng trụ đứng \(ABC.A'B'C'\) có đáy \(ABC\) là tam giác cân, với\(AB = AC = a\) và góc \(\widehat {BAC} = 120^\circ \), cạnh bên \(AA' = a\). Gọi \(I\) là trung điểm của \(CC'\). Cosin của góc tạo bởi hai mặt phẳng \(\left( {ABC} \right)\) và \(\left( {AB'I} \right)\) bằng
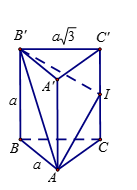
Ta có \(B{C^2} = A{B^2} + A{C^2} - 2AB.AC.\cos \widehat {BAC}\)\( = {a^2} + {a^2} - 2.a.a.\left( { - \dfrac{1}{2}} \right)\)\( = 3{a^2}\)\( \Rightarrow BC = a\sqrt[{}]{3}\).
Xét tam giác vuông \(B'AB\) có \(AB' = \sqrt[{}]{{B{{B'}^2} + A{B^2}}}\)\( = \sqrt[{}]{{{a^2} + {a^2}}}\)\( = a\sqrt[{}]{2}\).
Xét tam giác vuông \(IAC\) có \(IA = \sqrt[{}]{{I{C^2} + A{C^2}}}\)\( = \sqrt[{}]{{{a^2} + \dfrac{{{a^2}}}{4}}}\)\( = \dfrac{{a\sqrt[{}]{5}}}{2}\).
Xét tam giác vuông \(IB'C'\) có \(B'I = \sqrt[{}]{{B'{{C'}^2} + C'{I^2}}}\)\( = \sqrt[{}]{{3{a^2} + \dfrac{{{a^2}}}{4}}}\)\( = \dfrac{{a\sqrt[{}]{{13}}}}{2}\).
Xét tam giác \(IB'A\) có \(B'{A^2} + I{A^2} = 2{a^2} + \dfrac{{5{a^2}}}{4}\)\( = \dfrac{{13{a^2}}}{4}\)\( = B'{I^2}\)\( \Rightarrow \Delta IB'A\) vuông tại $A$
\( \Rightarrow \)${S_{IB'A}} = \dfrac{1}{2}AB'.AI$$ = \dfrac{1}{2}.a\sqrt[{}]{2}.\dfrac{{a\sqrt[{}]{5}}}{2}$$ = \dfrac{{{a^2}\sqrt[{}]{{10}}}}{4}$.
Lại có \({S_{ABC}} = \dfrac{1}{2}AB.AC.\sin \widehat {BAC}\)\( = \dfrac{1}{2}a.a.\dfrac{{\sqrt[{}]{3}}}{2}\)\( = \dfrac{{{a^2}\sqrt[{}]{3}}}{4}\).
Gọi góc tạo bởi hai mặt phẳng \(\left( {ABC} \right)\) và \(\left( {AB'I} \right)\)là \(\alpha \).
Ta có \(\Delta ABC\) là hình chiếu vuông góc của \(\Delta AB'I\) trên mặt phẳng \(\left( {ABC} \right)\).
Do đó \({S_{ABC}} = {S_{IB'A}}.\cos \alpha \)\( \Rightarrow \dfrac{{{a^2}\sqrt[{}]{3}}}{4} = \dfrac{{{a^2}\sqrt[{}]{{10}}}}{4}.\cos \alpha \)$ \Rightarrow \cos \alpha = \dfrac{{\sqrt[{}]{{30}}}}{{10}}$.
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $2a$. Gọi $O$ là giao điểm của $AC$ và $BD$. Biết hình chiếu vuông góc của đỉnh $S$ trên mặt phẳng $\left( {ABCD} \right)$ là trung điểm $H$ của đoạn $OA$ và góc $\widehat {\left( {SD;\left( {ABCD} \right)} \right)} = 60^\circ $. Gọi $\alpha $ là góc giữa hai mặt phẳng $\left( {SCD} \right)$ và $\left( {ABCD} \right)$. Tính $\tan \alpha $.
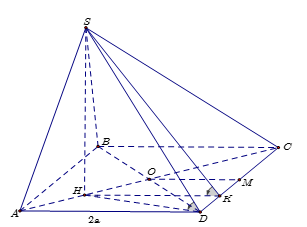
Ta có $SH \bot \left( {ABCD} \right)$ suy ra góc giữa $SD$ và mặt phẳng $\left( {ABCD} \right)$ chính là góc $\widehat {SDH}$ hay $\widehat {SDH} = 60^\circ $.
Hạ $HK \bot CD$ suy ra $CD \bot \left( {SHK} \right)$ nên góc giữa hai mặt phẳng $\left( {SCD} \right)$ và $\left( {ABCD} \right)$ là góc $\widehat {SKH}$ suy ra $\widehat {SKH} = \alpha $.
Ta có $DH = \sqrt {O{H^2} + O{D^2}} = \sqrt {{{\left( {\dfrac{{a\sqrt 2 }}{2}} \right)}^2} + {{\left( {a\sqrt 2 } \right)}^2}} = \dfrac{{a\sqrt 5 }}{{\sqrt 2 }}$.
Tam giác $SHD$ là nửa tam giác đều cạnh $SD = 2DH = a\sqrt {10} $ suy ra đường cao $SH = \dfrac{{\left( {a\sqrt {10} } \right)\sqrt 3 }}{2} = \dfrac{{a\sqrt {30} }}{2}$.
Gọi $M$ là trung điểm $CD$, ta có $HK = \dfrac{{OM + AD}}{2} = \dfrac{{3a}}{2}$.
Vậy $\tan \alpha = \dfrac{{SH}}{{HK}} = \dfrac{{\dfrac{{a\sqrt {30} }}{2}}}{{\dfrac{{3a}}{2}}} = \dfrac{{\sqrt {30} }}{3}$.
Cho hình hộp chữ nhật $ABCD.A'B'C'D'$ có các cạnh $AB = 2,\,\,AD = 3;\,AA' = 4$. Góc giữa hai mặt phẳng $\left( {AB'D'} \right)$ và $\left( {A'C'D} \right)$ là $\alpha $. Tính giá trị gần đúng của góc $\alpha $?
Cách 1: Hai mặt phẳng $\left( {AB'D'} \right)$ và $\left( {A'C'D} \right)$ có giao tuyến là $EF$ như hình vẽ. Từ $A'$ và $D'$ ta kẻ 2 đoạn vuông góc lên giao tuyến $EF$ sẽ là chung một điểm $H$ như hình vẽ. Khi đó, góc giữa hai mặt phẳng cần tìm chính là góc giữa hai đường thẳng $A'H$ và $D'H$.
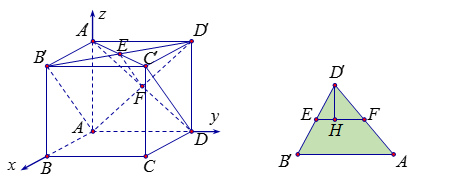
Tam giác $DEF$ lần lượt có $D'E = \dfrac{{D'B'}}{2} = \dfrac{{\sqrt {13} }}{2}$, $D'F = \dfrac{{D'A}}{2} = \dfrac{5}{2}$, $EF = \dfrac{{B'A}}{2} = \sqrt 5 $.
Theo hê rông ta có: ${S_{DEF}} = \dfrac{{\sqrt {61} }}{4}$. Suy ra $D'H = \dfrac{{2{S_{DEF}}}}{{EF}} = \dfrac{{\sqrt {305} }}{{10}}$.
Tam giác $D'A'H$ có: $\cos \widehat {A'HD'} = \dfrac{{H{{A'}^2} + H{{D'}^2} - A'{{D'}^2}}}{{2HA'.HD'}} = - \dfrac{{29}}{{61}}$.
Do đó $\widehat {A'HD'} \approx 118,4^\circ $ hay $\left( {\widehat {A'H,D'H}} \right) \approx 180^\circ - 118,4^\circ = 61,6^\circ $.
Cho hình chóp $S.ABC$ đáy $ABC$ là tam giác vuông cân với $BA = BC = a$, $SA = a$ và vuông góc với đáy, cosin góc giữa hai mặt phẳng $\left( {SAC} \right)$ và $\left( {SBC} \right)$ bằng:
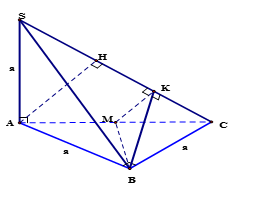
Cách 1:
Trong $\Delta SAC$, vẽ $AH \bot SC$
Gọi $M$ là trung điểm của $AC$, vẽ $MK \bot SC$ (1)
Vì $\Delta BAC$ vuông cân tại $B$ $ \Rightarrow $ $BM \bot AC$
Theo giả thiết $SA \bot \left( {ABC} \right) \Rightarrow SA \bot BM$
Ta có $\left\{ \begin{array}{l}BM \bot AC\\BM \bot SA\end{array} \right. \Rightarrow BM \bot \left( {SAC} \right) \Rightarrow BM \bot SC$ (2)
Từ (1) và (2) $ \Rightarrow $ $SC \bot \left( {BMK} \right) \Rightarrow SC \bot BK$ (3)
Từ (1) và (3) $ \Rightarrow $ $\left\{ \begin{array}{l}MK \bot SC;\,\,MK \subset \left( {SAC} \right)\\SC \bot BK;\,\,BK \subset \left( {SBC} \right)\end{array} \right.$
$ \Rightarrow $ $\left( {\left( {SAC} \right);\,\left( {SBC} \right)} \right) = \left( {BK;\,MK} \right) = \widehat {BKM}$
Vì tam giác $SBC$ vuông tại $B$, nên $\dfrac{1}{{B{K^2}}} = \dfrac{1}{{B{C^2}}} + \dfrac{1}{{B{A^2}}} = \dfrac{1}{{{a^2}}} + \dfrac{1}{{2{a^2}}} = \dfrac{3}{{2{a^2}}}\,\,\, \Rightarrow BK = \dfrac{{a\sqrt 6 }}{3}$
Vì $\Delta MCK \sim \Delta SCA$ $ \Rightarrow $ $\dfrac{{MK}}{{SA}} = \dfrac{{MC}}{{SC}} \Leftrightarrow MK = \dfrac{{MC.SA}}{{SC}} = \dfrac{{\dfrac{{a\sqrt 2 }}{2}.a}}{{a\sqrt 3 }} = \dfrac{{a\sqrt 6 }}{6}$
Theo CMT, ta có $BM \bot \left( {SAC} \right)$ $ \Rightarrow $ $BM \bot MK$ $ \Rightarrow $ $\Delta BMK$ vuông tại $M$
Do đó, $\cos \widehat {BMK} = \dfrac{{MK}}{{BK}} = \dfrac{{a\sqrt 6 }}{6}:\dfrac{{a\sqrt 6 }}{3} = \dfrac{1}{2}$
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật, \(AB = a\); \(AD = \dfrac{{a\sqrt 3 }}{2}\). Mặt bên \(SAB\) là tam giác cân đỉnh \(S\) và nằm trong mặt phẳng vuông góc với mặt phẳng \(\left( {ABCD} \right)\). Biết $\widehat {ASB} = 120^\circ $. Góc giữa hai mặt phẳng \(\left( {SAD} \right)\) và \(\left( {SBC} \right)\) bằng:
Gọi \(H\) là trung điểm của \(AB\), theo đề ra ta được \(SH \bot \left( {ABCD} \right)\).
Dựng \(T\), \(K\) lần lượt là hình chiếu của \(H\) lên \(SA\), \(SB\)\( \Rightarrow HT \bot \left( {SAD} \right)\) và \(HK \bot \left( {SBC} \right)\).
Vậy \(\left( {\widehat {\left( {SAD} \right);{\rm{ }}\left( {SBC} \right)}} \right) = \left( {\widehat {HT;{\rm{ }}HK}} \right)\).
Xét tứ giác \(SKHT\) có hai góc vuông đối diện nhau nên \(SKHT\) là tứ giác nội tiếp\( \Rightarrow \widehat {KHT} = 60^\circ \) do $\widehat {ASB} = 120^\circ $.
Vậy \(\left( {\widehat {\left( {SAD} \right);{\rm{ }}\left( {SBC} \right)}} \right) = \left( {\widehat {HT;{\rm{ }}HK}} \right) = \widehat {KHT} = 60^\circ \).

Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a\). Cạnh bên \(SA\) vuông góc với mặt phẳng đáy và có độ dài bằng \(a\sqrt 2 \). Gọi \(\alpha \) là góc giữa hai mặt phẳng \(\left( {SAD} \right)\) và \(\left( {SBD} \right)\). Tính \(\cos \alpha \).
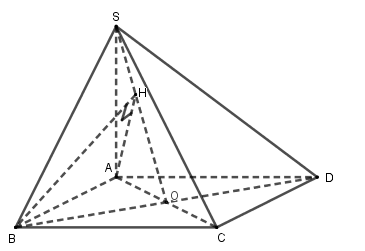
Gọi \(O\) là tâm hình vuông \(ABCD\). Kẻ \(AH \bot SO\) tại \(H\).
Ta có: \(BD \bot AO,\) \(BD \bot SA\)\( \Rightarrow BD \bot \left( {SAO} \right)\)\( \Rightarrow BD \bot AH\). Vậy \(AH \bot \left( {SBD} \right)\).
Lại có: \(AB \bot \left( {SAD} \right)\), do đó góc \(\alpha \) giữa hai mặt phẳng \(\left( {SAD} \right)\) và \(\left( {SBD} \right)\) là góc giữa hai đường thẳng \(AH\) và \(AB\). Do đó \(\alpha = \widehat {BAH}\) và \(\widehat {BAH} < {90^0} = \widehat {BHA}\).
Tam giác \(SAO\) vuông tại \(A\), đường cao \(AH\) nên: \(\dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{S^2}}} + \dfrac{1}{{A{O^2}}} = \dfrac{1}{{2{a^2}}} + \dfrac{4}{{2{a^2}}} = \dfrac{5}{{2{a^2}}}\)
Suy ra: \(AH = \dfrac{{a\sqrt {10} }}{5}\). Từ đó: \(\cos \alpha = \dfrac{{AH}}{{AB}} = \dfrac{{\sqrt {10} }}{5}\).
Cho hình chóp $S .A B C D$ có đáy là hình chữ nhật, \(AB = 2a,AD = a;\) tam giác $S A B$ đều và nằm trong mặt phẳng vuông góc với đáy. Góc \(\alpha \) tạo bởi hai mặt phẳng \((SCD)\) và \((ABCD)\) có số đo bằng
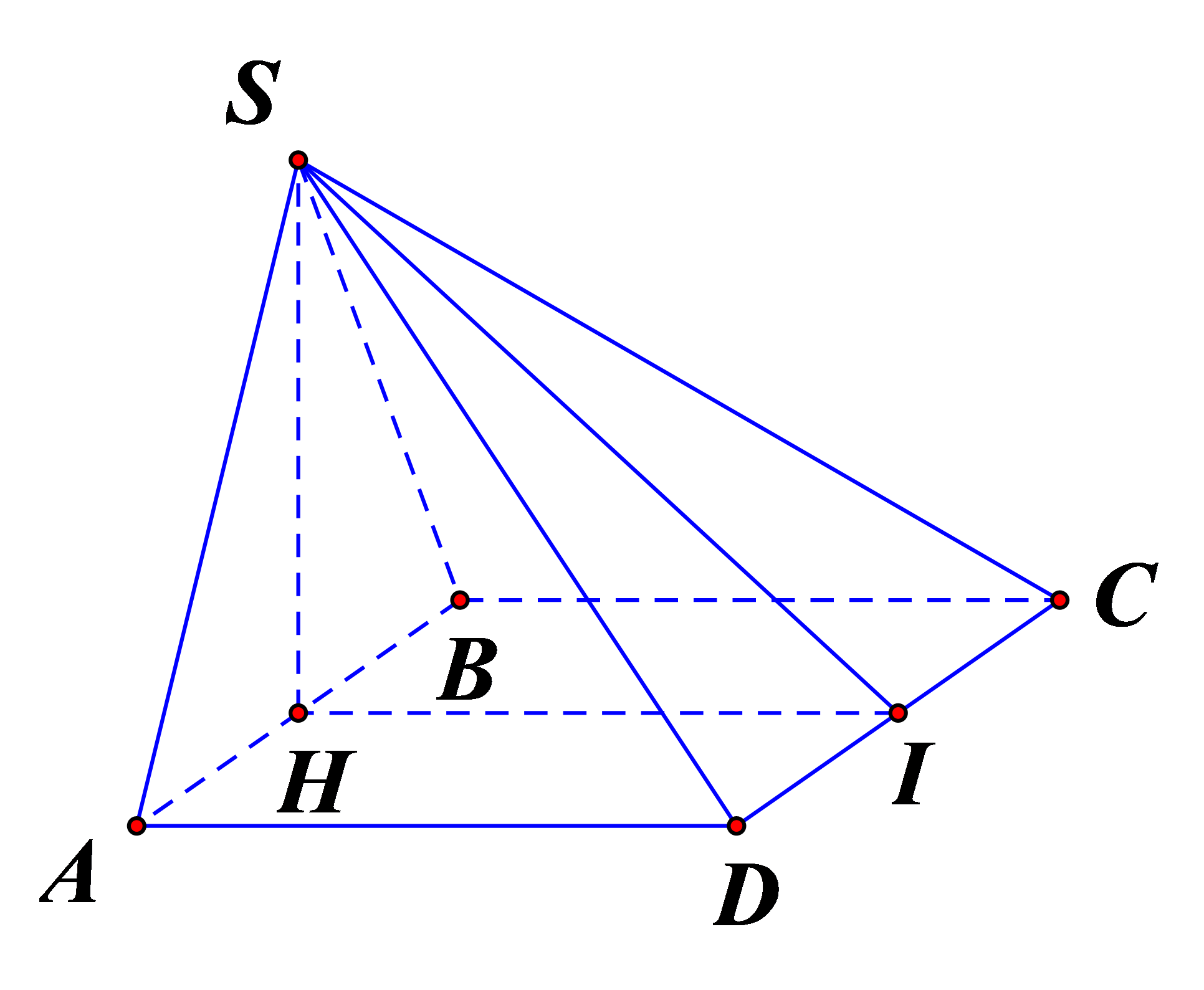
Gọi \(H\) là trung điểm $A B$, do tam giác $S A B$ đều nên \(SH \bot AB\). Mà \((SAB) \bot (ABCD)\) nên \(SH \bot (ABCD)\).
Gọi \(I\) là trung điểm $C D$.
Ta có: \(\alpha = ((SCD);(ABCD)) = \widehat {SIH}\).
Trong đó: $S H$ là đường cao của tam giác đều cạnh 2a nên \(SH = a\sqrt 3 ,HI = AD = a\).
Khi đó \(\tan \alpha = \tan \widehat {SIH} = \dfrac{{SH}}{{HI}} = \sqrt 3 \), suy ra \(\alpha = {60^0 }\).

