Trong mặt phẳng \(Oxy\), cho đường tròn $\left( C \right):{\left( {x - 6} \right)^2} + {\left( {y - 4} \right)^2} = 12$. Viết phương trình đường tròn là ảnh của đường tròn $\left( C \right)$ qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm \(O\) tỉ số $\dfrac{1}{2}$ và phép quay tâm \(O\) góc $90^\circ $.
Đường tròn $\left( C \right)$ có tâm \(I\left( {6;4} \right)\) và bán kính \(R = 2\sqrt 3 \).
Qua phép vị tự tâm \(O\) tỉ số $\dfrac{1}{2}$ điểm \(I\left( {6;4} \right)\) biến thành điểm \({I_1}\left( {3;2} \right)\); qua phép quay tâm \(O\) góc $90^\circ $ điểm \({I_1}\left( {3;2} \right)\) biến thành điểm \(I'\left( { - 2;3} \right)\).
Vậy ảnh của đường tròn $\left( C \right)$ qua phép đồng dạng trên là đường tròn có tâm \(I'\left( { - 2;3} \right)\) và bán kính \(R' = \dfrac{1}{2}R = \sqrt 3 \) có phương trình: ${\left( {x + 2} \right)^2} + {\left( {y - 3} \right)^2} = 3$.
Cho đường thẳng \(d\) có phương trình \(4x + 3y - 5 = 0\) và đường thẳng \(\Delta \) có phương trình \(x + 2y - 5 = 0\). Phương trình đường thẳng \(d'\) là ảnh của đường thẳng \(d\) qua phép đối xứng trục \(\Delta \) là
Gọi \(M = d \cap \Delta \)\( \Rightarrow M\left( { - 1;\;3} \right)\).
Lấy \(N\left( {2; - 1} \right) \in d\).
Gọi \({d_1}\) là đường thẳng qua \(N\) và vuông góc với \(\Delta \), ta có \({d_1}:2x - y - 5 = 0\)
Gọi \(I = {d_1} \cap \Delta \)\( \Rightarrow I\left( {3;\;1} \right)\).
Gọi \(N'\) là ảnh của \(N\) qua phép đối xứng trục \(\Delta \)\( \Rightarrow \) \(I\) là trung điểm của \(NN'\) nên \(N'\left( {4;\;3} \right)\).
\(d'\) là ảnh của đường thẳng \(d\) qua phép đối xứng trục \(\Delta \)
\( \Rightarrow \)\(d'\) là đường thẳng qua \(M\left( { - 1;\;3} \right)\) và \(N'\left( {4;\;3} \right)\).
Vậy \(d':y - 3 = 0\).
Thành phố Hải Đông dự định xây dựng một trạm nước sạch để cung cấp cho hai khu dân cư \(A\) và \(B\). Trạm nước sạch đặt tại vị trí\(C\) trên bờ sông. Biết \(AB = 3\sqrt {17} \,{\rm{km}}\), khoảng cách từ \(A\) và \(B\) đến bờ sông lần lượt là \(AM = 3\,{\rm{km}}\), \(BN = 6\,{\rm{km}} \)(hình vẽ). Gọi \(T\) là tổng độ dài đường ống từ trạm nước đến \(A\) và \(B\). Tìm giá trị nhỏ nhất của \(T\).
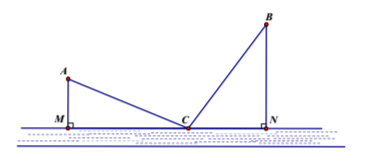
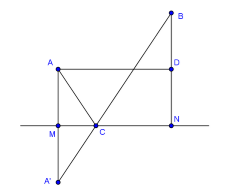
Gọi \(A'\) đối xứng với\(A\) qua \(MN\), \(D\) là trung điểm của \(NB\).
Do \(A\) cố định nên \(A'\) cũng cố định.
Ta có: \(T = CA + CB = CA' + CB \ge A'B\) (không đổi).
Đẳng thức xảy ra khi \(\left\{ C \right\} = MN \cap A'B\).
Khi đó: \(\dfrac{{MC}}{{NC}} = \dfrac{{MA'}}{{NB}} = \dfrac{{MA}}{{NB}} = \dfrac{1}{2}\) (1)
Mặt khác, \(MN = AD = \sqrt {A{B^2} - D{B^2}} \) \(= \sqrt {153 - 9} = 12 \,{\rm{km}}\) (2)
Từ (1) và (2) suy ra \(MC = 4\,km\), \(NC = 8 \,{\rm{km}}\).
Vậy \(T = CA + CB = \sqrt {A{M^2} + M{C^2}} + \sqrt {B{N^2} + N{C^2}}\) \( = \sqrt {9 + 16} + \sqrt {36 + 64} = 15\,{\rm{km}}\).
Trong mặt phẳng tọa độ $Oxy$, cho đường thẳng \(d:\)\(3x - y + 2 = 0\). Viết phương trình đường thẳng \(d'\) là ảnh của $d$ qua phép quay tâm $O$ góc quay \( - {90^{\rm{o}}}\).
Qua phép quay tâm $O$ góc quay \( - {90^{\rm{o}}}\) đường thẳng $d$ biến thành đường thẳng \(d'\) vuông góc với $d$.
Phương trình đường thẳng \(d'\) có dạng: \(x + 3y + m = 0\).
Lấy \(A\left( {0;2} \right) \in d\). Qua phép quay tâm $O$ góc quay \( - {90^{\rm{o}}}\), điểm \(A\left( {0;2} \right)\) biến thành điểm \(B\left( {2;0} \right) \in d'\). Khi đó \(m = - 2\).
Vậy phương trình đường \(d'\) là \(x + 3y - 2 = 0\).
Trong mặt phẳng tọa độ $Oxy$, cho hai đường tròn $\left( C \right):{\left( {x + m} \right)^2} + {\left( {y - 2} \right)^2} = 5$ và $\left( {C'} \right):{x^2} + {y^2} + 2\left( {m - 2} \right)x - 6y + 12 + {m^2} = 0$. Vectơ $\overrightarrow v $ nào dưới đây là vectơ của phép tịnh tiến biến $\left( C \right)$ thành $\left( {C'} \right)$?
Điều kiện để $\left( {C'} \right)$ là đường tròn ${\left( {m - 2} \right)^2} + 9 - 12 - {m^2} > 0 \Leftrightarrow - 4m + 1 > 0 \Leftrightarrow m < \dfrac{1}{4}$.
Khi đó:
Đường tròn $\left( {C'} \right)$ có tâm là $I'\left( {\,2 - m;\,\,3} \right)$, bán kính $R' = \sqrt { - 4m + 1} $.
Đường tròn $\left( C \right)$ có tâm là $I\left( { - m;\,2} \right)$, bán kính $R = \sqrt 5 $.
Phép tịnh tiến theo vectơ $\overrightarrow v $ biến $\left( C \right)$ thành $\left( {C'} \right)$ khi và chỉ khi $\left\{ \begin{array}{l}R' = R\\\overrightarrow {II'} = \overrightarrow v \end{array} \right.$
$ \Leftrightarrow \left\{ \begin{array}{l}\sqrt { - 4m + 1} = \sqrt 5 \\\overrightarrow v = \overrightarrow {II'} \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m = - 1\\\overrightarrow v = \left( {2;\,1} \right)\end{array} \right.$.
Vậy chọn A
Trong mặt phẳng \(Oxy\) cho đường tròn \(\left( C \right)\) có phương trình \({\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} = 4.\) Hỏi phép vị tự tâm \(O\) tỉ số \(k = - 2\) biến \(\left( C \right)\) thành đường tròn nào sau đây:

Gọi \(\left( {C'} \right)\) là ảnh của đường tròn \(\left( C \right)\) qua phép vị tự tâm \(O\) tỉ số \(k = - 2\).
Đường tròn \(\left( C \right)\) có tâm \(I\left( {1;2} \right)\) và bán kính \(R = 2\).
Gọi \(I'\) và $R'$ tâm và bán kính của đường tròn \(\left( {C'} \right)\).
Ta có: \(R' = \left| k \right|R = \left| { - 2} \right|.2 = 4\).
Mặt khác: \(\overrightarrow {OI'} = - 2\overrightarrow {OI} \Leftrightarrow \left\{ \begin{array}{l}{x_{I'}} = - 2{x_I} = - 2.1 = - 2\\{y_{I'}} = - 2{y_I} = - 2.2 = - 4\end{array} \right. \Rightarrow I'\left( { - 2; - 4} \right)\)
Vậy, phương trình đường tròn \(\left( {C'} \right)\) là \({\left( {x + 2} \right)^2} + {\left( {y + 4} \right)^2} = 16.\)
Cho ba điểm \(A\), \(B\), \(C\) thẳng hàng theo thứ tự đó và \(AB = 2BC\). Dựng các hình vuông \(ABEF\), \(BCGH\) (đỉnh của hình vuông tính theo chiều kim đồng hồ). Xét phép quay tâm \(B\) góc quay \( - 90^\circ \) biến điểm \(E\) thành điểm \(A.\) Gọi \(I\) là giao điểm của \(EC\) và \(GH.\) Giả sử \(I\) biến thành điểm \(J\) qua phép quay trên. Nếu \(AC = 3\) thì \(IJ\) bằng
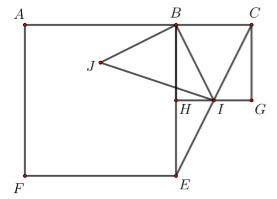
Do \(Q\left( {B; - 90^\circ } \right):I \to J\) nên \(\Delta BIJ\) vuông cân tại \(B\) \( \Rightarrow IJ = BI\sqrt 2 \).
Mà \(AC = 3\) \( \Rightarrow BC = 1\). Vì \(AB = 2BC\) \( \Rightarrow BE = 2BH\) \( \Rightarrow \) \(HI\) là đường trung bình \(\Delta EBC\)
\( \Rightarrow HI = \dfrac{1}{2}BC = \dfrac{1}{2}\). Ta có \(BI = \sqrt {B{H^2} + I{H^2}} = \sqrt {1 + \dfrac{1}{4}} = \dfrac{{\sqrt 5 }}{2}\)
Vậy $IJ = BH\sqrt 2 = \dfrac{{\sqrt {10} }}{2}$.
Trong mặt phẳng \(Oxy\), tìm phương trình đường tròn \(\left( {C'} \right)\) là ảnh của đường tròn \(\left( C \right)\): \({x^2} + {y^2} = 1\) qua phép đối xứng tâm \(I\left( {1;\;0} \right)\).
Đường tròn \(\left( C \right)\) có tâm \(O\left( {0;\;0} \right)\), bán kính \(R = 1\).
Gọi \(O'\) là ảnh của \(O\) qua phép đối xứng tâm \(I\left( {1;\;0} \right)\).
Ta có: $\left\{ {\begin{array}{*{20}{c}}{\dfrac{{{x_O} + {x_{O'}}}}{2} = {x_I}}\\{\dfrac{{{y_O} + {y_{O'}}}}{2} = {y_I}}\end{array}} \right.$$ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{x_{O'}} = 2{x_I} - {x_O}}\\{{y_{O'}} = 2{y_I} - {y_O}}\end{array}} \right.$$ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{x_{O'}} = 2.1 - 0}\\{{y_{O'}} = 2.0 - 0}\end{array}} \right.$$ \Rightarrow O'\left( {2;\;0} \right)$.
Đường tròn \(\left( {C'} \right)\) là ảnh của đường tròn \(\left( C \right)\) qua phép đối xứng tâm \(I\left( {1;\;0} \right)\).
\(\left( {C'} \right)\) có tâm $O'\left( {2;\;0} \right)$, bán kính \(R' = R = 1\).
Phương trình đường tròn \(\left( {C'} \right)\) là: \({\left( {x - 2} \right)^2} + {y^2} = 1\).
Trong mặt phẳng tọa độ \(Oxy\), phép quay tâm \(O\) góc quay \(90^\circ \) biến điểm \(M\left( { - 1;\;2} \right)\) thành điểm \(M'\). Tọa độ điểm \(M'\) là
Có \(M' = {Q_{\left( {O;90^\circ } \right)}}\left( M \right) \Leftrightarrow \left\{ \begin{array}{l}\left( {OM;\;OM'} \right) = 90^\circ \\OM' = OM\end{array} \right.\).
Phương trình đường thẳng $OM'$ qua \(O\), vuông góc với \(OM\) nên \(OM'\) có dạng $x - 2y = 0$.
Gọi \(M'\left( {2a;\;a} \right)\). Do \(OM' = OM\)\( \Rightarrow 4{a^2} + {a^2} = {\left( { - 1} \right)^2} + {2^2}\)\( \Leftrightarrow \left[ \begin{array}{l}a = 1\\a = - 1\end{array} \right.\)\( \Rightarrow \left[ \begin{array}{l}M'\left( {2;\;1} \right)\\M'\left( { - 2;\; - 1} \right)\end{array} \right.\).
Có \(M'\left( {2;\;1} \right)\) là ảnh của \(M\) qua phép quay góc \( - 90^\circ \), \(M'\left( { - 2;\; - 1} \right)\) là ảnh của \(M\) qua phép quay góc \(90^\circ \). Vậy chọn \(M'\left( { - 2;\; - 1} \right)\).
Ảnh của điểm \(M\left( {2; - 3} \right)\) qua phép quay tâm \(I\left( { - 1;2} \right)\) góc quay \(120^\circ \) là
Gọi \(M'\left( {x';y'} \right)\) là ảnh của \(M\left( {2; - 3} \right)\) qua phép quay tâm \(I\left( { - 1;2} \right)\) góc quay \(120^\circ \)
Ta có: \(\left\{ {\begin{array}{*{20}{c}}{x' = \left( {x - a} \right)\cos \varphi - \left( {y - b} \right)\sin \varphi + a}\\{x' = \left( {x - a} \right)\sin \varphi + \left( {y - b} \right)\cos \varphi + b}\end{array}} \right.\)\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x' = \left( {2 + 1} \right)\cos 120^\circ - \left( { - 3 - 2} \right)\sin 120^\circ - 1}\\{x' = \left( {2 + 1} \right)\sin 120^\circ + \left( { - 3 - 2} \right)\cos 120^\circ + 2}\end{array}} \right.\).
$ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x' = - \dfrac{3}{2} + 5\dfrac{{\sqrt 3 }}{2} - 1}\\{y' = 3.\dfrac{{\sqrt 3 }}{2} + \dfrac{5}{2} + 2}\end{array}} \right.$$ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x' = \dfrac{{5\sqrt 3 - 5}}{2}}\\{y' = \dfrac{{3\sqrt 3 + 9}}{2}}\end{array}} \right.$. Vậy \(M'\left( {\dfrac{{5\sqrt 3 - 5}}{2};\dfrac{{3\sqrt 3 + 9}}{2}} \right)\).
Trong mặt phẳng tọa độ \(Oxy\), cho tam giác \(ABC\) có trực tâm \(O\). Gọi \(M\) là trung điểm của \(BC\); \(N\), \(P\) lần lượt là chân đường cao kẻ từ \(B\) và \(C\). Đường tròn đi qua ba điểm \(M\), \(N\), \(P\) có phương trình là \(\left( T \right):{\left( {x - 1} \right)^2} + {\left( {y + \dfrac{1}{2}} \right)^2} = \dfrac{{25}}{4}\). Phương trình đường tròn ngoại tiếp tam giác \(ABC\) là:
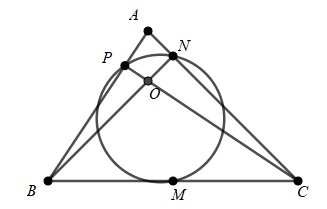
Gọi \(I\) và \(I'\) lần lượt là tâm đường tròn ngoại tiếp tam giác \(MNP\) và tam giác \(ABC\).
Gọi \(R\) và \(R'\) lần lượt là bán kính đường tròn ngoại tiếp tam giác \(MNP\) và tam giác \(ABC\).
Ta có \(I\left( {1; - \dfrac{1}{2}} \right)\) và do đó \(\overrightarrow {OI'} = 2\overrightarrow {OI} \Rightarrow I'\left( {2;\; - 1} \right)\).
Mặt khác \(R = \dfrac{5}{2} \Rightarrow R' = 5\).
Vậy phương trình đường tròn ngoại tiếp tam giác \(ABC\) là: \({\left( {x - 2} \right)^2} + {\left( {y + 1} \right)^2} = 25\).

