Trong các khẳng định sau đây khẳng định nào đúng?
A. Sai vì có thể cắt hoặc chéo nhau.
C. Sai vì hai mặt phẳng đó có thể trùng nhau hoặc cắt nhau.
D. Sai vì hai mặt phẳng đó có thể cắt nhau.
Trong các khẳng định sau khẳng định nào là đúng?
Theo định nghĩa: Hình lăng trụ đều là hình lăng trụ đứng có đáy là một đa giác đều.
Trong các khẳng định sau khẳng định nào đúng?
Dựa vào định nghĩa hình chóp đều và tính chất hình chóp đều ta chọn đáp án A.
Cắt hình chóp tứ giác bởi mặt phẳng vuông góc với đường cao của hình chóp thiết diện là hình gì?
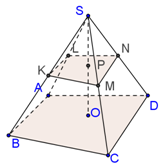
Quan sát hình vẽ ta thấy, thiết diện là một tứ giác đồng dạng với tứ giác ở đáy.
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật với $AB = a$, $AD = 2a$, $SA = 3a$ và $SA$ vuông góc với mặt đáy. Góc giữa đường thẳng $SD$ và mặt phẳng $\left( {ABCD} \right)$ là
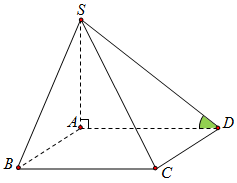
Ta có $SA \bot \left( {ABCD} \right)$.
\( \Rightarrow AD\) là hình chiếu vuông góc của \(SD\) xuống mặt \(\left( {ABCD} \right)\).
\( \Rightarrow \left( {\widehat {SD,\,\,\left( {ABCD} \right)}} \right) = \left( {\widehat {SD,\,\,AD}} \right) = \widehat {SDA}\).
Cho tứ diện $ABCD$ có $AB$, $AC$, $AD$ đôi một vuông góc với nhau. Số đo góc giữa hai đường thẳng $AB$ và $CD$ bằng
Vì \(\left. \begin{array}{l}AB \bot AC\\AB \bot AD\end{array} \right\} \Rightarrow AB \bot \left( {ACD} \right) \Rightarrow AB \bot CD\).
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác đều cạnh \(a\), \(SA\) vuông góc với mặt phẳng đáy và \(SA = \dfrac{a}{2}\). Tính khoảng cách giữa hai đường thẳng \(SA\) và \(BC\).
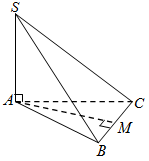
Gọi \(M\) là trung điểm cạnh \(BC\).
Ta có $\left\{ \begin{array}{l}AM \bot BC\\AM \bot SA\end{array} \right. \Rightarrow AM$ là đoạn vuông góc chung của hai đường thẳng \(SA\) và \(BC\).
Do đó \(AM = d\left( {SA,\,\,BC} \right) = \dfrac{{a\sqrt 3 }}{2}\).
Cho tứ diện $ABCD$ có $AB = AC$ và $DB = DC$. Khẳng định nào sau đây đúng?
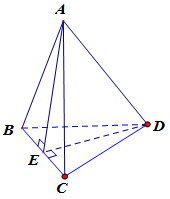
Gọi \(E\) là trung điểm của \(BC\).
Tam giác \(ABC\) cân nên \(BC \bot AE\);
Tam giác \(DBC\) cân nên \(BC \bot DE\).
Do đó \(BC \bot \left( {AED} \right) \Rightarrow BC \bot AD\).
Chọn mệnh đề đúng trong các mệnh đề sau đây:
Chỉ có A đúng còn lại B, C, D là sai.
Cho hình chóp \(S.ABCD\) có đáy là hình bình hành, cạnh bên \(SA\) vuông góc với đáy. Biết khoảng cách từ \(A\) đến \(\left( {SBD} \right)\) bằng \(\dfrac{{6a}}{7}\). Tính khoảng cách từ \(C\) đến mặt phẳng \(\left( {SBD} \right)\)?
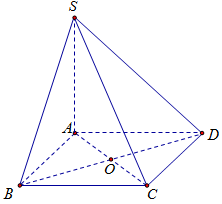
Do \(ABCD\) là hình bình hành\( \Rightarrow AC \cap BD = O\) là trung điểm của \(AC\) và \(BD\)\( \Rightarrow d\left( {C,\left( {SBD} \right)} \right) = d\left( {A,\left( {SBD} \right)} \right) = \dfrac{{6a}}{7}\).
Cho hình lập phương \(ABCD.A'B'C'D'\). Góc giữa hai đường thẳng \(BA'\) và \(CD\) bằng:
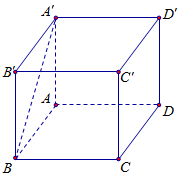
Có $CD{\rm{//}}AB \Rightarrow \left( {BA',CD} \right) = \left( {BA',BA} \right) = \widehat {ABA'} = 45^\circ $ (do \(ABB'A'\) là hình vuông).
Cho hình chóp \(S.ABC\) có \(SA = SB = SC = AB = AC = a\), \(BC = a\sqrt 2 \). Tính số đo của góc giữa hai đường thẳng \(AB\) và \(SC\) ta được kết quả:
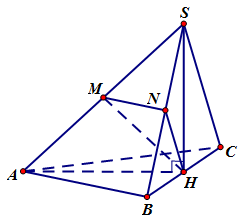
Gọi $H$ là hình chiếu vuông góc của $S$ lên mặt phẳng \(\left( {ABC} \right)\), theo đầu bài \(SA = SB = SC\) và tam giác \(\Delta ABC\) vuông cân tại \(A\) ta có \(H\) là trung điểm của \(BC\). Gọi \(M\), \(N\) lần lượt là trung điểm của \(SA\), \(SB\) ta có: \(\left\{ \begin{array}{l}MN\;{\rm{//}}\;AB\\HN\;{\rm{//}}\;SC\end{array} \right.\)
\( \Rightarrow \) Góc giữa \(AB\) và \(SC\) là góc giữa \(MN\) và \(HN\).
Xét tam giác \(\Delta MNH\) ta có: \(MN = \dfrac{{AB}}{2} = \dfrac{a}{2};\) \(HN = \dfrac{{SC}}{2} = \dfrac{a}{2}\;;\) \(MH = \dfrac{{SA}}{2} = \dfrac{a}{2}\)
(do \(\Delta SHA\) vuông tại \(H\))
\( \Rightarrow \) tam giác \(\Delta MNH\) là tam giác đều \( \Rightarrow \)\(\widehat {MNH} = 60^\circ \).
Vậy góc cần tìm là \(60^\circ \).
Cho tứ diện \(ABCD\) có \(AB = AC = 2,\)\(DB = DC = 3\). Khẳng định nào sau đây đúng?
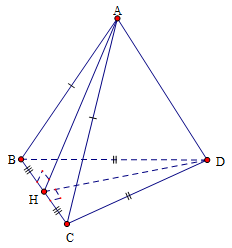
Theo đề bài ta có: \(\Delta ABC,\) \(\Delta DBC\) lần lượt cân tại \(A,\)\(D\). Gọi \(H\) là trung điểm của \(BC\).
\( \Rightarrow \left\{ \begin{array}{l}AH \bot BC\\DH \bot BC\end{array} \right.\)\( \Rightarrow \left\{ \begin{array}{l}AD \subset \left( {ADH} \right)\\BC \bot \left( {ADH} \right)\end{array} \right.\)\( \Rightarrow BC \bot AD\).
Cho hình lăng trụ đứng $ABC.A'B'C'$ có đáy là tam giác $ABC$ vuông tại $A$ có $BC = 2a$, $AB = a\sqrt 3 $. Khoảng cách từ $AA'$ đến mặt phẳng $\left( {BCC'B'} \right)$ là:
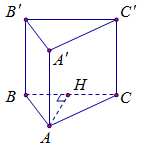
Ta có $AA'{\rm{//}}\left( {BCC'B'} \right)$ nên khoảng cách từ $AA'$ đến mặt phẳng $\left( {BCC'B'} \right)$ cũng chính là khoảng cách từ $A$ đến mặt phẳng $\left( {BCC'B'} \right)$.
Hạ $AH \bot BC \Rightarrow AH \bot \left( {BCC'B'} \right)$.
Ta có $\dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{C^2}}} = \dfrac{1}{{3{a^2}}} + \dfrac{1}{{B{C^2} - A{B^2}}} = \dfrac{1}{{3{a^2}}} + \dfrac{1}{{{a^2}}} = \dfrac{4}{{3{a^2}}}$$ \Rightarrow AH = \dfrac{{a\sqrt 3 }}{2}$.
Vậy khoảng cách từ $AA'$ đến mặt phẳng $\left( {BCC'B'} \right)$ bằng $\dfrac{{a\sqrt 3 }}{2}$.
Cho hình chóp $S.ABCD$có đáy $ABCD$ là hình vuông cạnh $a$, cạnh bên $SA$ vuông góc với mặt đáy và \(SA = a\sqrt 2 \). Tìm số đo của góc giữa đường thẳng $SC$ và mặt phẳng$\left( {SAB} \right)$.
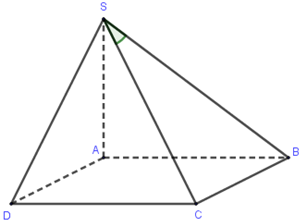
Dễ thấy $CB \bot \left( {SAB} \right)$ $ \Rightarrow SB$ là hình chiếu vuông góc của $SC$ lên $\left( {SAB} \right)$.
Vậy góc giữa đường thẳng $SC$ và mặt phẳng $\left( {SAB} \right)$ là $\widehat {CSB}$.
Tam giác $CSB$ có $\widehat B = 90^\circ ;\,CB = a;\,SB = a\sqrt 3 \Rightarrow \tan \widehat {CSB} = \dfrac{{CB}}{{SB}} = \dfrac{a}{{a\sqrt 3 }} = \dfrac{1}{{\sqrt 3 }}$.
Vậy $\widehat {CSB}$ \( = 30^\circ \).
Cho hình chóp $S.ABCD$ có tất cả các cạnh bên và cạnh đáy đều bằng $a$ và $ABCD$ là hình vuông. Gọi $M$ là trung điểm của $CD.$ Giá trị \(\overrightarrow {MS} .\overrightarrow {CB} \) bằng
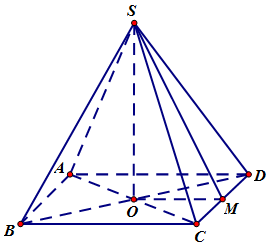
Do tất cả các cạnh của hình chóp bằng nhau nên hình chóp \(S.ABCD\) là hình chóp đều \( \Rightarrow \left\{ \begin{array}{l}SO \bot (ABCD)\\AC \bot BD\end{array} \right.\).
Do M là trung điểm của CD nên ta có:
\(\overrightarrow {MS} = \overrightarrow {{\rm{O}}S} - \overrightarrow {OM} = - \dfrac{1}{2}\overrightarrow {OC} - \dfrac{1}{2}\overrightarrow {OD} + \overrightarrow {{\rm{O}}S} \), \(\overrightarrow {CB} = \overrightarrow {OB} - \overrightarrow {OC} = - \overrightarrow {OD} - \overrightarrow {OC} \).
Do \(\overrightarrow {OC} ;\) \(\overrightarrow {OS} ;\) \(\overrightarrow {OD} \) đôi một vuông góc với nhau nên ta có:
\(\overrightarrow {MS} .\overrightarrow {CB} = \dfrac{1}{2}O{C^2} + \dfrac{1}{2}O{D^2} = O{C^2} = \dfrac{{{a^2}}}{2}\)
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh bằng \(1\). Tam giác \(SAB\) đều và nằm trong mặt phẳng vuông góc với mặt đáy \(\left( {ABCD} \right)\). Tính khoảng cách từ \(B\) đến \(\left( {SCD} \right).\)
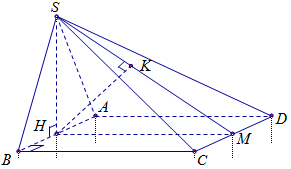
Gọi \(H\), \(M\) lần lượt là trung điểm của \(AB\) và \(CD\) suy ra \(HM = 1\), \(SH = \dfrac{{\sqrt 3 }}{2}\) và \(SM = \dfrac{{\sqrt 7 }}{2}\)
Vì tam giác \(SAB\) đều và nằm trong mặt phẳng vuông góc với đáy \(\left( {ABCD} \right)\) nên \(SH \bot \left( {ABCD} \right)\).
Vì \(AB{\rm{//C}}D\) nên \(AB{\rm{//}}\left( {SCD} \right)\).
Do đó \(d\left( {B;\,\left( {SCD} \right)} \right) = d\left( {H;\,\left( {SCD} \right)} \right) = HK\) với \(HK \bot SM\) trong \(\Delta SHM\).
Ta có:\(\dfrac{1}{{H{K^2}}} = \dfrac{1}{{S{H^2}}} + \dfrac{1}{{H{M^2}}}\)\( \Rightarrow HK = \dfrac{{\sqrt {21} }}{7}\).
Cho hình chóp \(S.ABC\) có \(AB = AC\), \(\widehat {SAC} = \widehat {SAB}\). Tính số đo của góc giữa hai đường thẳng \(SA\) và \(BC.\)
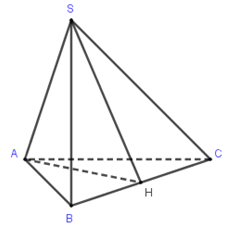
Vì \(AB = AC\), \(\widehat {SAC} = \widehat {SAB}\) nên \(\Delta \,SAC = \Delta \,SAB\), suy ra \(SB = SC\), nên hai tam giác \(ABC\) và \(SBC\) là tam giác cân. Gọi \(H\) là trung điểm \(BC\), ta có \(\left\{ \begin{array}{l}AH \bot BC\\SH \bot BC\end{array} \right. \Rightarrow \left( {SAH} \right) \bot BC\).
Vậy \(SA \bot BC\).
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật với \(AB = 2a\), \(BC = a\). Các cạnh bên của hình chóp cùng bằng $a\sqrt 2 $. Tính góc giữa hai đường thẳng \(AB\) và \(SC\).
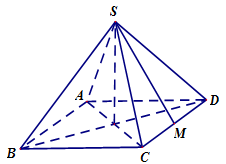
Ta có \(AB{\rm{//}}CD\) nên $\left( {\widehat {AB;\,SC}} \right) = \left( {\widehat {CD;\,SC}} \right) = \widehat {SCD}$.
Gọi \(M\) là trung điểm của \(CD\).
Tam giác \(SCM\) vuông tại \(M\) và có \(SC = a\sqrt 2 \), \(CM = a\) nên là tam giác vuông cân tại \(M\) nên $\widehat {SCD} = 45^\circ $.
Vậy $\left( {\widehat {AB;\,SC}} \right) = 45^\circ $.
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông tâm \(O\) cạnh \(a\), \(SO\) vuông góc với mặt phẳng \(\left( {ABCD} \right)\) và \(SO = a.\) Khoảng cách giữa \(SC\) và \(AB\) bằng
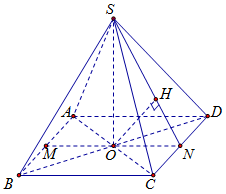
Gọi \(M,N\) lần lượt là trung điểm của các cạnh $AB,CD$; $H$ là hình chiếu vuông góc của \(O\) trên \(SN.\)
Vì $AB{\rm{//}}CD$ nên \(d\left( {AB,SC} \right) = d\left( {AB,(SCD)} \right) = d\left( {M,(SCD)} \right) = 2d\left( {O,(SCD)} \right)\) (vì \(O\) là trung điểm đoạn \(MN\))
Ta có $\left\{ \begin{array}{l}CD \bot SO\\CD \bot ON\end{array} \right. \Rightarrow CD \bot (SON) \Rightarrow CD \bot OH$
Khi đó $\left\{ \begin{array}{l}CD \bot OH\\OH \bot SN\end{array} \right. \Rightarrow OH \bot (SCD) \Rightarrow d\left( {O;(SCD)} \right) = OH.$
Tam giác \(SON\) vuông tại \(O\) nên $\dfrac{1}{{O{H^2}}} = \dfrac{1}{{O{N^2}}} + \dfrac{1}{{O{S^2}}} = \dfrac{1}{{\dfrac{{{a^2}}}{4}}} + \dfrac{1}{{{a^2}}} = \dfrac{5}{{{a^2}}} \Rightarrow OH = \dfrac{a}{{\sqrt 5 }}$
Vậy \(d\left( {AB,SC} \right) = 2OH = \dfrac{{2a\sqrt 5 }}{5}\).

