Trong không gian, cho hai đường thẳng phân biệt a, b và mặt phẳng \(\alpha \). Phát hiểu nào sau đây đúng?
Nếu \(b//(\alpha )\) và \(a \bot (\alpha )\) thì \(a \bot b\).
Cho hình chóp S.ABCD có đáy là hình thoi, cạnh bên SA vuông góc với mặt phẳng (ABCD) (như hình vẽ minh họa)
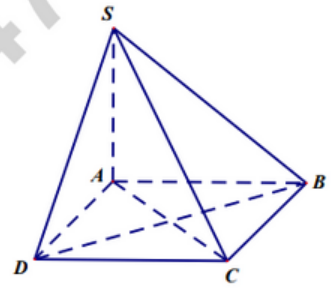
Hãy chọn khẳng định đúng?
ABCD là hình thoi nên \(BD \bot AC\).
Mà \(BD \bot SA\) và AC và SA cắt nhau tại A nên \(BD \bot \left( {SAC} \right)\).
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác cân tại \(A\), cạnh bên \(SA\) vuông góc với đáy, \(M\) là trung điểm của \(BC\), \(J\) là trung điểm của \(BM\). Mệnh đề nào sau đây là đúng?
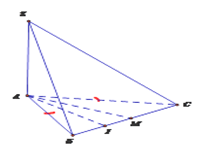
\(\Delta ABC\) cân tại A
\(\left. \begin{array}{l} \Rightarrow BC \bot AM\\BC \bot SA\left( {SA \bot \left( {ABCD} \right)} \right)\end{array} \right\}\)\( \Rightarrow BC \bot \left( {SAM} \right)\)
Cho hình chóp \(S.ABCD\) có đáy là hình chữ nhật và \(SA\) vuông góc với đáy. Khi đó số mặt bên của hình chóp là tam giác vuông bằng :
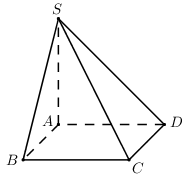
Ta có :
\(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot AB\)\( \Rightarrow \Delta SAB\) vuông tại \(A\).
\(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot AD\)\( \Rightarrow \Delta SAD\) vuông tại \(A\).
Ta có \(\left\{ \begin{array}{l}BC \bot AB\\BC \bot SA\left( {SA \bot \left( {ABCD} \right)} \right)\end{array} \right.\)
\( \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow BC \bot SB\)
\( \Rightarrow \Delta SBC\) vuông tại \(B\).
\(\left\{ \begin{array}{l}CD \bot AD\\CD \bot SA\,\,\left( {SA \bot \left( {ABCD} \right)} \right)\end{array} \right.\)\( \Rightarrow CD \bot \left( {SAD} \right) \Rightarrow CD \bot SD\)\( \Rightarrow \Delta SCD\) vuông tại \(D\).
Vậy cả bốn mặt của hình chóp đều là tam giác vuông.
Khẳng định nào sau đây sai?
Đường thẳng \(d\) vuông góc với hai đường thẳng nằm trong \(\left( \alpha \right)\) thì \(d \bot \left( \alpha \right)\) chỉ đúng khi hai đường thẳng đó cắt nhau.
Cho hai đường thẳng \(a,b\) và \(mp\left( P \right)\). Chỉ ra mệnh đề đúng trong các mệnh đề sau:
Câu A sai vì \(b\) có thể nằm trong \(\left( P \right)\) .
Câu B đúng bởi \(a//\left( P \right) \Rightarrow \exists a' \subset \left( P \right)\) sao cho \(a//a',b \bot \left( P \right) \Rightarrow b \bot a'\). Khi đó \(a \bot b\).
Câu C sai vì \(b\) có thể nằm trong \(\left( P \right)\).
Câu D sai vì \(b\) có thể nằm trong \(\left( P \right)\).
Qua điểm $O$ cho trước, có bao nhiêu mặt phẳng vuông góc với đường thẳng \(\Delta \) cho trước?
Theo tiên đề qua điểm $O$ cho trước có duy nhất một mặt phẳng vuông góc với đường thẳng $\Delta $
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông tại $B,$ cạnh bên $SA$ vuông góc với đáy. Gọi $H$ là chân đường cao kẻ từ $A$ của tam giác $SAB.$ Khẳng định nào dưới đây là sai ?
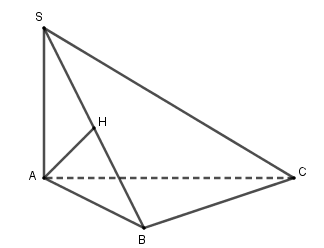
Theo bài ra, ta có $SA \bot \left( {ABC} \right)$ mà $BC \subset \left( {ABC} \right) \Rightarrow SA \bot BC.$
Tam giác $ABC$ vuông tại $B,$ có $AB \bot BC$$ \Rightarrow $$BC \bot \left( {SAB} \right) \Rightarrow BC \bot AH.$
Khi đó $\left\{ \begin{array}{l}AH \bot SB\\AH \bot BC\end{array} \right. \Rightarrow AH \bot \left( {SBC} \right) \Rightarrow AH \bot SC.$
Nếu $AH \bot AC$ mà $SA \bot AC$ suy ra $AC \bot \left( {SAH} \right) \Rightarrow AC \bot AB$ (vô lý).
Trong các mệnh đề sau, mệnh đề nào đúng?
Đáp án A: Có vô số đường thẳng đi qua 1 điểm và vuông góc với một đường thẳng cho trước nên A sai.
Đáp án B: Nếu đường thẳng đã cho vuông góc với mặt phẳng đã cho thì có vô số mặt phẳng đi qua đường thẳng này và vuông góc với mặt phẳng kia nên B sai.
Đáp án C: đúng.
Đáp án D: Qua một điểm cho trước có thể kẻ được vô số mặt phẳng vuông góc với mặt phẳng cho trước nên D sai.
Cho tứ diện \(OABC\) có \(OA,{\rm{ }}OB,{\rm{ }}OC\) đôi một vuông góc với nhau. Gọi \(H\) là hình chiếu của \(O\) trên mặt phẳng \(\left( {ABC} \right)\). Mệnh đề nào sau đây là sai?
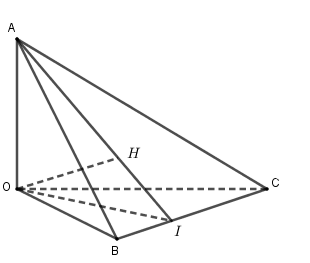
+) \(\left\{ \begin{array}{l}OA \bot OB\\OA \bot OC\end{array} \right. \Rightarrow OA \bot \left( {OBC} \right) \Rightarrow OA \bot BC.\) Do đó A đúng.
+) Do \(OH \bot \left( {ABC} \right)\) nên \(OH \bot AB\) nên B đúng.
Gọi \(I = AH \cap BC.\)
Theo giả thiết ta có $OH \bot \left( {ABC} \right) \Rightarrow OH \bot BC.$ Suy ra \(BC \bot \left( {AOI} \right)\) \( \Rightarrow BC \bot OI,BC \bot AI\)
Gọi \(J = BH \cap AC.\) Chứng minh tương tự ta có \(AC \bot BJ\).
Suy ra $H$ là trực tâm \(\Delta ABC.\) Do đó C đúng.
Vậy D là đáp án sai vì \(AO \bot \left( {OBC} \right)\) và \(AO \ne AH\).
Cho $a,b,c$ là các đường thẳng trong không gian. Tìm mệnh đề sai trong các mệnh đề sau.
Nếu \(\left\{ \begin{array}{l}a \bot b\\b \bot c\end{array} \right.\) thì \(a,c\) có thể cắt nhau, trùng nhau, song song nên đáp án A sai.
Ví dụ:
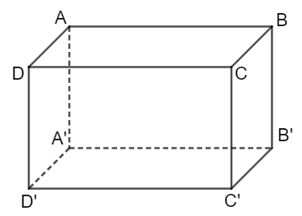
Hình hộp chữ nhật $ABCD.A'B'C'D'$ có AD vuông góc với AA' và AA' vuông góc với A'B' nhưng AD và A'B' không song song với nhau mà là vuông góc với nhau.
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thoi tâm $O.$ Cạnh bên $SA$ vuông góc với đáy. Khẳng định nào sau đây là sai ?
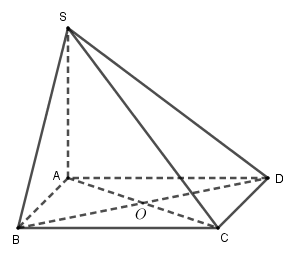
Vì $SA$ vuông góc với $mp\,\,\left( {ABCD} \right)\,\,\, \Rightarrow \,\,SA \bot BD.$
Mà $ABCD$ là hình thoi tâm $O$$ \Rightarrow $$AC \bot BD$ nên suy ra $BD \bot \left( {SAC} \right).$
Mặt khác $SO \subset \left( {SAC} \right)$ và $SC \subset \left( {SAC} \right)$ suy ra $\left\{ \begin{array}{l}BD \bot SO\\BD \bot SC\end{array} \right.$.
Và $AD,\,\,\,SC$ là hai đường thẳng chéo nhau.
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông tại $B,$ cạnh bên $SA$ vuông góc với đáy. Gọi $O$ là tâm đường tròn ngoại tiếp tam giác $SBC.$ $H$ là hình chiếu của $O$ trên $\left( {ABC} \right).$ Khẳng định nào dưới đây đúng ?

Ta có $SA$ vuông góc với $mp\,\,\left( {ABC} \right) \Rightarrow SA \bot BC$ mà $AB \bot BC$ suy ra $BC \bot \left( {SAB} \right)$
$ \Rightarrow \,\,\,BC \bot SB\,\,\, \Rightarrow $ tam giác $SBC$ vuông tại $B\,\, \Rightarrow $$O$là trung điểm của $SC.$
Theo bài ra, ta có $OH \bot \left( {ABC} \right)\,\, \Rightarrow \,\,OH$//$SA \Rightarrow \,\,H$ là trung điểm của $AC.$
Mà tam giác $ABC$ vuông tại $B$ nên $H$ là tâm đường tròn ngoại tiếp tam giác $ABC.$
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật tâm $O.$ Đường thẳng \(SA\) cuông góc với mặt đáy \(\left( {ABCD} \right)\). Gọi $I$ là trung điểm của $SC.$ Khẳng định nào dưới đây là sai ?
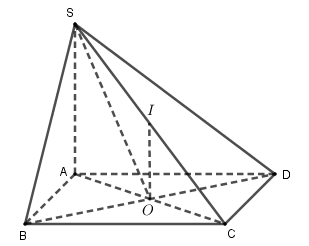
Vì $O,\,\,I$ lần lượt là trung điểm của $AC,\,\,SC$ suy ra $OI$ là đường trung bình của tam giác $SAC$$ \Rightarrow $$OI$//$SA$ mà $SA \bot \left( {ABCD} \right) \Rightarrow OI \bot \left( {ABCD} \right).$
Ta có $ABCD$ là hình chữ nhật $ \Rightarrow \,\,\,BC \bot AB$ mà $SA \bot BC$ suy ra $BC \bot SB.$
Tương tự, ta có được $\left\{ \begin{array}{l}CD \bot AD\\CD \bot SA\,\,\,\,\,\left( {SA \bot \left( {ABCD} \right)} \right)\end{array} \right. \Rightarrow CD \bot SD.$
Nếu $\left( {SAC} \right)$ là mặt phẳng trung trực của $BD\,\, \Rightarrow \,BD \bot AC$: điều này không thể xảy ra vì $ABCD$ là hình chữ nhật.
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật, cạnh bên $SA$ vuông góc với mặt phẳng đáy. Gọi $AE,\,\,AF$ lần lượt là đường cao của tam giác $SAB$ và tam giác $SAD.$ Khẳng định nào dưới đây là đúng ?

Vì $SA$ vuông góc với mặt phẳng $\left( {ABCD} \right)$$ \Rightarrow $$SA \bot BC.$
Mà $AB \bot BC$ nên suy ra $BC \bot \left( {SAB} \right) \Rightarrow BC \bot AE \subset \left( {SAB} \right).$
Tam giác $SAB$ có đường cao $AE$$ \Rightarrow \,\,AE \bot SB$ mà $AE \bot BC \Rightarrow AE \bot \left( {SBC} \right) \Rightarrow AE \bot SC.$
Tương tự, ta chứng minh được $AF \bot SC$. Do đó $SC \bot \left( {AEF} \right).$
Cho hình chóp \(S.ABCD\) với đáy \(ABCD\) là hình thang vuông tại \(A\) và \(D\) , có \(AD = CD = a\), \(AB = 2a\). Cạnh bên \(SA\) vuông góc với đáy \(\left( {ABCD} \right)\), \(E\) là trung điểm của \(AB\). Chỉ ra mệnh đề sai trong các mệnh đề sau:
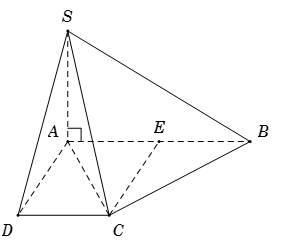
Từ giả thết suy ra \(ADCE\) là hình vuông \( \Rightarrow \left\{ \begin{array}{l}CE \bot AB\\CE = AD = a\end{array} \right..\)
Ta có \(\left\{ \begin{array}{l}CE \bot AB\\CE \bot SA{\rm{ }}\left( {{\rm{do }}SA \bot ABCD} \right)\end{array} \right. \Rightarrow CE \bot \left( {SAB} \right).\) Do đó A đúng.
Vì \(CE = AD = a \Rightarrow CE = \dfrac{1}{2}AB \Rightarrow \Delta ABC\) vuông tại \(C \Rightarrow CB \bot AB\). Kết hợp với \(CB \bot SA\) (do \(SA \bot \left( {ABCD} \right)\)) nên suy ra \(CB \bot \left( {SAC} \right).\) Do đó B đúng.
Ta có \(\left\{ \begin{array}{l}CD \bot AD\\CD \bot SA{\rm{ }}\left( {{\rm{do }}SA \bot ABCD} \right)\end{array} \right. \Rightarrow CD \bot \left( {SAD} \right) \Rightarrow CD \bot SD.\) Do đó C đúng.
Dùng phương pháp loại trừ, suy ra D là đáp án sai.
Trong không gian, cho đoạn thẳng AB có trung điểm là I, \((\alpha )\) là mặt phẳng trung trực của đoạn thẳng AB. Phát biểu nào sau đây đúng?
Mặt phẳng trung trực của đoạn thẳng AB là mặt phẳng vuông góc với AB tại trung điểm của AB.
Cho hai đường thẳng phân biệt $a,{\rm{ }}b$ và mặt phẳng$\left( P \right)$, trong đó $a \bot \left( P \right)$. Mệnh đề nào sau đây là sai?
Các đáp án A, B, C đúng.
Đáp án D sai vì có thể xảy ra trường hợp \(b\) nằm trong \(\left( P \right)\).
Trong không gian cho đường thẳng \(\Delta \) và điểm \(O.\) Qua \(O\) có mấy đường thẳng vuông góc với $\Delta$ cho trước?
Qua điểm \(O\) có thể dựng vô số đường thẳng vuông góc với \(\Delta \), các đường thẳng đó cùng nằm trong một mặt phẳng vuông góc với \(\Delta \).
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác cân tại \(C.\) Cạnh bên \(SA\) vuông góc với đáy. Gọi \(H,\,\,K\) lần lượt là trung điểm của \(AB\) và \(SB.\) Khẳng định nào dưới đây sai ?
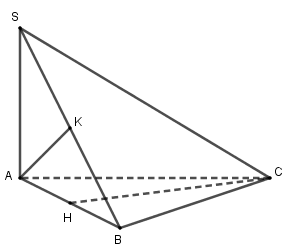
Vì \(H\) là trung điểm của \(AB\), tam giác \(ABC\) cân suy ra \(CH \bot AB.\)
Ta có \(SA \bot \left( {ABC} \right) \Rightarrow SA \bot CH\) mà \(CH \bot AB\) suy ra \(CH \bot \left( {SAB} \right).\)
Mặt khác \(AK \subset \left( {SAB} \right)\)\( \Rightarrow \,\,CH\) vuông góc với các đường thẳng \(SA,\,\,SB,\,\,AK.\)
Và \(AK \bot SB\) chỉ xảy ra khi và chỉ khi tam giác \(SAB\) cân tại \(S.\)

