Cho góc nhọn $xOy$ và điểm $A$ thuộc miền trong của góc đó, điểm $B$ thuộc cạnh $Ox$ ($B$ khác $O$). Tìm $C$ thuộc $Oy$ sao cho chu vi tam giác $ABC$ nhỏ nhất?
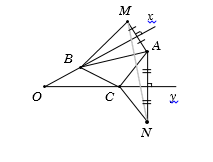
Gọi $M$ là điểm đối xứng với $A$ qua $Ox.$ Vì $B \in Ox$ nên suy ra $BA = BM.$
Gọi $N$ là điểm đối xứng với $A$ qua $Oy$. Vì $C \in Oy$ nên suy ra $CA = CN.$
Chu vi tam giác: ${P_{\Delta ABC}} = AB + BC + CA = BM + BC + CN.$ \(\left( * \right)\)
Theo bất đẳng thức tam giác mở rộng, ta có
$MB + BC \ge MC$ và $MC + CN \ge MN.$
Kết hợp với $\left( * \right)$, suy ra
${P_{\Delta ABC}} = \left( {MB + BC} \right) + CN \ge MC + CN \ge MN.$
Dấu xảy ra khi và chỉ khi $B,\,\,C,\,\,M,\,\,N$ thẳng hàng hay $C$ là giao điểm của $BM$ với trục $Oy$.
Trong mặt phẳng $Oxy$ cho đường thẳng $d$ có phương trình \(x - y + 1 = 0\) và hai điểm\(A\left( {3;1} \right);B\left( {7;5} \right)\). Tìm điểm $M$ thuộc $d$ sao cho \(MA + MB\) nhỏ nhất ?
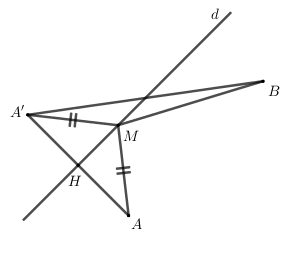
Ta dễ dàng kiểm tra được $A,B$ nằm cùng phía so với đường thẳng $d$.
Gọi $A'$ là điểm đối xứng với $A$ qua $d$ , ta có : \(MA = MA'\)
\( \Rightarrow MA + MB = MA' + MB \ge A'B\)
\( \Rightarrow MA + MB\) nhỏ nhất \( \Leftrightarrow M,A',B\) thẳng hàng hay \(M = A'B \cap d\).
Đường thẳng $AA'$ đi qua $A$ và vuông góc với $d$ nên có phương trình \(x + y - 4 = 0\,\,\left( {d'} \right)\).
Gọi \(H = d \cap d' \Rightarrow \) Tọa độ điểm $H$ là nghiệm của hệ
$\left\{ \begin{array}{l}x - y + 1 = 0\\x + y - 4 = 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x = \dfrac{3}{2}\\y = \dfrac{5}{2}\end{array} \right. \Rightarrow H\left( {\dfrac{3}{2};\dfrac{5}{2}} \right)$ là trung điểm của \(AA' \Rightarrow \left\{ \begin{array}{l}{x_{A'}} = 2{x_H} - {x_A} = 0\\{y_{A'}} = 2{y_H} - {y_H} = 4\end{array} \right. \Rightarrow A'\left( {0;4} \right)\)
\( \Rightarrow \) Phương trình đường thẳng $A'B$ là : \(\dfrac{{x - 0}}{{7 - 0}} = \dfrac{{y - 4}}{{5 - 4}} \Leftrightarrow \dfrac{x}{7} = y - 4 \Leftrightarrow x - 7y + 28 = 0\)
\( \Rightarrow MA + MB\) nhỏ nhất \( \Leftrightarrow M = A'B \cap d \Rightarrow \) Tọa độ điểm $M$ là nghiệm của hệ \(\left\{ \begin{array}{l}x - y + 1 = 0\\x - 7y + 28 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{7}{2}\\y = \dfrac{9}{2}\end{array} \right. \Rightarrow M\left( {\dfrac{7}{2};\dfrac{9}{2}} \right)\) .
Cho tam giác $ABC$ có $A$ là góc nhọn và các đường cao là $AA',\,\,BB',\,\,CC'.$ Gọi $H$ là trực tâm tam giác \(ABC\) và $H'$ là điểm đối xứng của $H$ qua $BC.$ Tứ giác nào sau đây là tứ giác nội tiếp ?
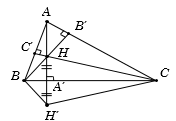
Vì $H'$ đối xứng với $H$ qua $BC$ suy ra $\widehat {BHC} = \widehat {BH'C}.$
Mặt khác $\widehat {BHC} = \widehat {B'HC'}$ (hai góc đối đỉnh).
Suy ra $\widehat {BH'C} = \widehat {B'HC'}\,.$ $\left( 1 \right)$
Ta có $\left\{ \begin{array}{l}BB' \bot AC\\CC' \bot AB\end{array} \right. \Rightarrow \widehat {AC'H} = \widehat {AB'H} = {90^0}$
\( \Rightarrow \) tứ giác $AB'HC'$ là tứ giác nội tiếp.
Suy ra $\widehat {B'AC'} + \widehat {B'HC'} = {180^0}.$ $\,\left( 2 \right)$
Từ $\left( 1 \right)$ và $\left( 2 \right)$, suy ra $\widehat {BH'C} + \widehat {BAC} = {180^0}.$
Vậy tứ giác $ABH'C$ là tứ giác nội tiếp
Trong mặt phẳng tọa độ \(Oxy\), cho đường thẳng \(d:\,\,2x - y + 7 = 0\) và \(d':\,\,2x - y + 13 = 0.\) Tìm phép đối xứng qua trục biến \(d\) thành \(d'.\)
Gọi \({D_\Delta }\left( d \right) = d'\).
Nhận xét: \(d\parallel d'\), do đó \(\Delta \) là đường thẳng song song cách đều \(d\) và \(d'\).
Vậy \(\Delta :\,\,2x - y + 10 = 0\).
Tìm ảnh của \(d:x - y + 1 = 0\) qua phép đối xứng trục \(\Delta :2x - y = 0.\)
Gọi \(d' = {D_\Delta }\left( d \right)\).
Gọi \(A = d \cap \Delta \Rightarrow A\left( {1;2} \right)\).
Do \(A \in \Delta \Rightarrow {D_\Delta }\left( A \right) = A\)\( \Rightarrow A \in d'\).
Chọn \(B\left( {0;1} \right) \in d\), tìm \(B' = {d_\Delta }\left( B \right)\).
Gọi \(\Delta '\) là đường thẳng đi qua \(B\) và vuông góc với \(\Delta \)\( \Rightarrow \Delta ':\,\,x + 2y + c = 0\).
\(B\left( {0;1} \right) \in \Delta ' \Rightarrow 0 + 2 + c = 0 \Leftrightarrow c = - 2\)\( \Rightarrow \Delta ':\,\,x + 2y - 2 = 0\).
Gọi \(H = \Delta \cap \Delta ' \Rightarrow H\left( {\dfrac{2}{5};\dfrac{4}{5}} \right)\).
\(B' = {D_d}\left( B \right) \Rightarrow H\) là trung điểm của \(BB'\).
\( \Rightarrow B' = 2H - B \Rightarrow B'\left( {\dfrac{4}{5};\dfrac{3}{5}} \right)\).
Đường thẳng \(d'\) đi qua \(A,\,\,B'\) nhận \(\overrightarrow {AB'} = \left( { - \dfrac{1}{5}; - \dfrac{7}{5}} \right)\parallel \left( {1;7} \right)\) là 1 VTCP.
\( \Rightarrow d':\,\,7\left( {x - 1} \right) - 1\left( {y - 2} \right) = 0\)\( \Leftrightarrow 7x - y - 5 = 0\).
Đường thẳng đối xứng với đường thẳng \(d:\left\{ \begin{array}{l}x = 1 - 2t\\y = 2 + t\end{array} \right.\) qua đường thẳng \(\Delta :x + 2y = 0\) có phương trình là:
Ta có: \(d:\left\{ \begin{array}{l}x = 1 - 2t\\y = 2 + t\end{array} \right. \Rightarrow x + 2y - 5 = 0\)
Mà \(\Delta :x + 2y = 0 \Rightarrow d\parallel \Delta .\)
+ Gọi \(d'\) là đường thẳng đối xứng với \(d\) qua \(\Delta \) \( \Rightarrow d'\) cũng song song \(\Delta \).
\( \Rightarrow \) Đường thẳng \(d'\) có dạng: \(x + 2y + c = 0\).
+ Trên \(d\) lấy điểm \(A\left( {5;0} \right)\). Trên \(\Delta \) lấy điểm \(I\left( {2; - 1} \right)\).
+ Gọi \(A' \in d'\) là điểm đối xứng với \(A\) qua \(I\) \( \Rightarrow I\) là trung điểm của \(AA'\).
\( \Leftrightarrow \left\{ \begin{array}{l}{x_I} = \dfrac{{{x_A} + {x_{A'}}}}{2}\\{y_I} = \dfrac{{{y_A} + {y_{A'}}}}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_{A'}} = 2{x_I} - {x_A}\\{y_{A'}} = 2{y_I} - {y_A}\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}{x_{A'}} = - 1\\{y_{A'}} = - 2\end{array} \right. \Rightarrow A'\left( { - 1; - 2} \right)\)
Mà \(A' \in d' \Rightarrow x + 2y + c = 0\)\( \Leftrightarrow - 1 - 4 + c = 0 \Leftrightarrow c = 5.\)
Vậy phương trình đường thẳng \(d'\) là \(x + 2y + 5 = 0\).
Trong mặt phẳng tọa độ \(Oxy\), cho \(A\left( {1;2} \right);\,\,B\left( {4;4} \right)\). Tìm điểm \(M\) thuộc \(Ox\) sao cho \(MA + MB\) nhỏ nhất?
+ Dễ thấy \(A,B\) nằm cùng phía so với trục \(Ox\).
+ Gọi \(A' = \) Đ\(_{Ox}\left( A \right) \Rightarrow A'\left( {1; - 2} \right)\); khi đó ta có \(MA = MA'\).
\( \Rightarrow MA + MB = MA' + MB \ge A'B\).
Dấu "=" xảy ra \( \Leftrightarrow M,\,\,A',\,\,B\) thẳng hàng hay \(M = A'B \cap Ox\).
+ Phương trình \(A'B:\,\,\frac{{x - 1}}{{4 - 1}} = \frac{{y + 2}}{{4 + 2}} \Leftrightarrow 2\left( {x - 1} \right) = y + 2 \Leftrightarrow 2x - y - 4 = 0\).
+ Tọa độ của \(M\) là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}2x - y - 4 = 0\\y = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 0\end{array} \right. \Rightarrow M\left( {2;0} \right)\).
Trong mặt phẳng tọa độ \(Oxy\), cho parabol \(\left( P \right):\,\,{y^2} = - 12x\). Hỏi parabol nào là ảnh của \(\left( P \right)\) qua phép đối xứng trục \(Ox\)?
Đ\(_{Ox}\left[ {M\left( {x;y} \right)} \right] = M'\left( {x';y'} \right)\)
\(\Rightarrow \left\{ \begin{array}{l}x' = x\\y' = - y\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x = x'\\y = - y'\end{array} \right. \Rightarrow M\left( {x'; - y'} \right)\)
Thay \(M\) vào \(\left( P \right)\) ta có \(y{'^2} = - 12x'\).
Đ\(_{Ox}\left( P \right) = \left( {P'} \right) \)
\(\Rightarrow \left( {P'} \right):\,\,{y^2} = - 12x\).
Hình nào sau đây là có trục đối xứng:
Trong bốn đáp án chỉ có tam giác cân là hình có trục đối xứng.
Cho hình vuông \(ABCD\) có hai đường chéo \(AC\) và \(BD\) cắt nhau tại \(I\). Khẳng định nào sau đây là đúng về phép đối xứng trục:
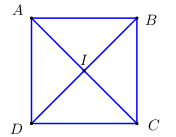
Do \(ABCD\) nên hai đường chéo \(AC \bot BD\) và \(AC \cap BD\) tại trung điểm của mỗi đường.
\( \Rightarrow AC\) là trung trực của \(BD \Rightarrow \) Đ\(_{AC}\left( D \right) = B\).
Trong mặt phẳng tọa độ \(C'\left( {4;16} \right)\), gọi $a$ là đường thẳng có phương trình $x + 2 = 0.$ Phép đối xứng trục biến điểm $M\left( {4; - 3} \right)$ thành $M'$ có tọa độ là:
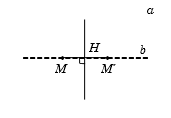
Đường thẳng $b$ qua $M$ và vuông góc với $a$ có phương trình $b:y + 3 = 0.$
Gọi $H = a \cap b,$ tọa độ điểm $H$ là nghiệm của hệ $\left\{ \begin{array}{l}x + 2 = 0\\y + 3 = 0\end{array} \right. \Rightarrow H\left( { - 2; - 3} \right).$
Theo giả thiết: ${D_a}\left( M \right) = M'\left( {x';y'} \right) \Rightarrow H$ là trung điểm của $MM'$
$ \Leftrightarrow \left\{ \begin{array}{l}x' = 2{x_H} - {x_M}\\y' = 2{y_H} - {y_M}\end{array} \right.$$ \Rightarrow \left\{ \begin{array}{l}x' = - 8\\y' = - 3\end{array} \right. \Rightarrow M'\left( { - 8; - 3} \right)$
Trong mặt phẳng tọa độ \(Oxy\), cho đường thẳng $\Delta $ có phương trình $2x - y + 1 = 0$ và điểm $A\left( {3;2} \right).$ Trong các điểm dưới đây, điểm nào là điểm đối xứng của $A$ qua đường thẳng $\Delta ?$
Đường thẳng $d$ qua $A$ và vuông góc với $\Delta $ có phương trình $d:x + 2y - 7 = 0$
Gọi $H = d \cap \Delta ,$ tọa độ điểm $H$ là nghiệm của hệ $\left\{ \begin{array}{l}2x - y + 1 = 0\\x + 2y - 7 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = 3\end{array} \right. \Rightarrow H\left( {1;3} \right).$
Theo giả thiết: là trung điểm của $AA'$
$ \Leftrightarrow \left\{ \begin{array}{l}x' = 2{x_H} - {x_A}\\y' = 2{y_H} - {y_A}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x' = - 1\\y' = 4\end{array} \right. \Rightarrow A'\left( { - 1;4} \right).$
Cho ba đường tròn có bán kính bằng nhau và đôi một tiếp xúc ngoài với nhau tạo thành hình $H$. Hỏi $H$ có mấy trục đối xứng?
Có 3 trục đối xứng như hình vẽ.
Tam giác đều có bao nhiêu trục đối xứng?
Tam giác đều có $3$ trục đối xứng (đường thẳng đi qua đỉnh tam giác và trung điểm cạnh đối diện).
Trong các hình sau đây, hình nào có bốn trục đối xứng?
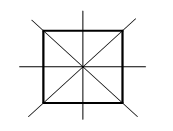
Hình vuông có bốn 4 trục đối xứng. (đường chéo và đường thẳng đi qua trung điểm của cặp cạnh đối diện).
Trong mặt phẳng tọa độ \(C'\left( {4;16} \right).\) cho tam giác \(ABC\) với \(A\left( {1;5} \right),\) \(B\left( { - 1;2} \right),\) \(C\left( {6; - 4} \right).\) Gọi $G$ là trọng tâm của tam giác \(ABC.\) Phép đối xứng trục ${D_{Oy}}$ biến điểm \(G\) thành điểm \(G'\) có tọa độ là:
Tọa độ trọng tâm: \(\left\{ \begin{array}{l}{x_G} = \dfrac{{{x_A} + {x_B} + {x_C}}}{3}\\{y_G} = \dfrac{{{y_A} + {y_B} + {y_C}}}{3}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{x_G} = 2\\{y_G} = 1\end{array} \right. \Rightarrow G\left( {2;1} \right).\)
Gọi \(G'\left( {x';y'} \right) = \)${D_{Oy}}\left[ {G\left( {x;y} \right)} \right]$ thì \(\left\{ \begin{array}{l}x' = - x\\y' = y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x' = - 2\\y' = 1\end{array} \right..\)
Trong mặt phẳng tọa độ \(Oxy\) cho điểm $M\left( {2;3} \right)$. Hỏi trong bốn điểm sau điểm nào là ảnh của \(M\) qua phép đối xứng trục \(Ox?\)
Biểu thức tọa độ qua phép đối xứng trục \(Ox\):
Gọi \(M'\left( {x';y'} \right) = \)${D_{Ox}}\left[ {M\left( {x;y} \right)} \right]$ thì \(\left\{ \begin{array}{l}x' = x\\y' = - y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x' = 2\\y' = - 3\end{array} \right..\)
Trong mặt phẳng tọa độ \(C'\left( {4;16} \right).\) qua phép đối xứng trục \(Oy\), điểm $A\left( {3;5} \right)$ biến thành điểm nào trong các điểm sau?
Biểu thức tọa độ qua phép đối xứng trục \(Oy\):
Gọi \(A'\left( {x';y'} \right) = \)${D_{Oy}}\left[ {A\left( {x;y} \right)} \right]$ thì$\left\{ \begin{array}{l}x' = - x\\y' = y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x' = - 3\\y' = 5\end{array} \right.$.
Trong các hình dưới đây, hình nào có nhiều trục đối xứng nhất?
Đoạn thẳng có 1 trục đối xứng là đường trung trực của đoạn thẳng.
Đường tròn có vô số trục đối xứng là các đường thẳng đi qua tâm.
Tam giác đều có 3 trục đối xứng là các đường thẳng đi qua đỉnh và trung điểm cạnh đối diện.
Hình vuông có 4 trục đối xứng.
Vậy hình tròn có nhiều trục đối xứng nhất.
Trong mặt phẳng tọa độ \(Oxy\) cho đường tròn $\left( C \right):{\left( {x + 1} \right)^2} + {\left( {y - 4} \right)^2} = 1$ và đường thẳng \(d\) có phương trình $y - x = 0.$ Phép đối xứng trục \(d\) biến đường tròn \(\left( C \right)\) thành đường tròn $\left( {C'} \right)$ có phương trình là:
Biểu thức tọa độ của phép đối xứng qua trục $d:y - x = 0$ (đường phân giác góc phần tư thứ nhất) là $\left\{ {\begin{array}{*{20}{c}}{x' = y}\\{y' = x}\end{array}} \right.$.
Thay vào $\left( C \right)$, ta được ${\left( {y' + 1} \right)^2} + {\left( {x' - 4} \right)^2} = 1$ hay ${\left( {x - 4} \right)^2} + {\left( {y + 1} \right)^2} = 1.$
