Câu hỏi:
2 năm trước
Cho tam giác $ABC$ có $A$ là góc nhọn và các đường cao là $AA',\,\,BB',\,\,CC'.$ Gọi $H$ là trực tâm tam giác \(ABC\) và $H'$ là điểm đối xứng của $H$ qua $BC.$ Tứ giác nào sau đây là tứ giác nội tiếp ?
Trả lời bởi giáo viên
Đáp án đúng: b
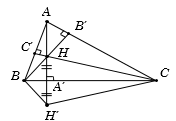
Vì $H'$ đối xứng với $H$ qua $BC$ suy ra $\widehat {BHC} = \widehat {BH'C}.$
Mặt khác $\widehat {BHC} = \widehat {B'HC'}$ (hai góc đối đỉnh).
Suy ra $\widehat {BH'C} = \widehat {B'HC'}\,.$ $\left( 1 \right)$
Ta có $\left\{ \begin{array}{l}BB' \bot AC\\CC' \bot AB\end{array} \right. \Rightarrow \widehat {AC'H} = \widehat {AB'H} = {90^0}$
\( \Rightarrow \) tứ giác $AB'HC'$ là tứ giác nội tiếp.
Suy ra $\widehat {B'AC'} + \widehat {B'HC'} = {180^0}.$ $\,\left( 2 \right)$
Từ $\left( 1 \right)$ và $\left( 2 \right)$, suy ra $\widehat {BH'C} + \widehat {BAC} = {180^0}.$
Vậy tứ giác $ABH'C$ là tứ giác nội tiếp
Hướng dẫn giải:
Sử dụng dấu hiệu nhận biết tứ giác nội tiếp: Tổng hai góc đối bằng \({180^0}\).
